Capítulo 5 Enzimas

      De modo geral, enzimas são estudadas sob diversos pontos de vista, tais como sua estrutura, mecanismo de ação, e comportamento cinético. Este capítulo visa trabalhar nesse último, com auxílio do R.
      De modo geral, a equação simplificada que descreve a atividade de uma enzima E sobre um substrato S pode ser descrita como:

\[\begin{equation} E+S \begin{array}{c} _{k1}\\ \rightleftharpoons\\ ^{k2} \end{array} ES \begin{array}{c} _{k3}\\ \rightarrow \\ ^{}\end{array}E+P \tag{5.1} \end{equation}\]

Onde P representa o produto da reação, ES o complexo ativado no estado de transição, e k1, k2 e k3 as constantes de velocidade da reação.

      Pela aproximação de Briggs-Haldane para o estado estacionário, e o tratamento de Henri-Michaelis-Menten, a equação que define a curva de velocidade da reação enzimática em função do teor de substrato pode ser descrita abaixo:

\[\begin{equation} v=\frac{Vm*S}{Km+S} \tag{5.2} \end{equation}\]

Onde Km representa a constante de Michaelis-Menten, e Vm a velocidade limite da reação (por vezes denominada erroneamente como velocidade máxima, embora a hipérbole quadrática descrita pela função não exiba valor máximo por não atingir uma assíntota). Por sua vez Km pode ser definido a partir das constantes de velocidade da equação (5.1) como:

\[\begin{equation} Km=\frac{k1+k3}{k2} \tag{5.2} \end{equation}\]

      Portanto, dados os valores de Vm e Km, podemos descrever um comportamento de Michaelis-Menten para uma enzima como:

Vm= 10
Km = 0.5
curve(Vm*x/(Km+x),xlim=c(0,10),
      xlab="[S]", ylab="v")
abline(h=5,lty=2,col="blue")
abline(v=0.5,lty=2, col="blue")
text(x=1,y=0.2,"Km",col="blue")
text(1,5.3,"Vm/2",col="blue")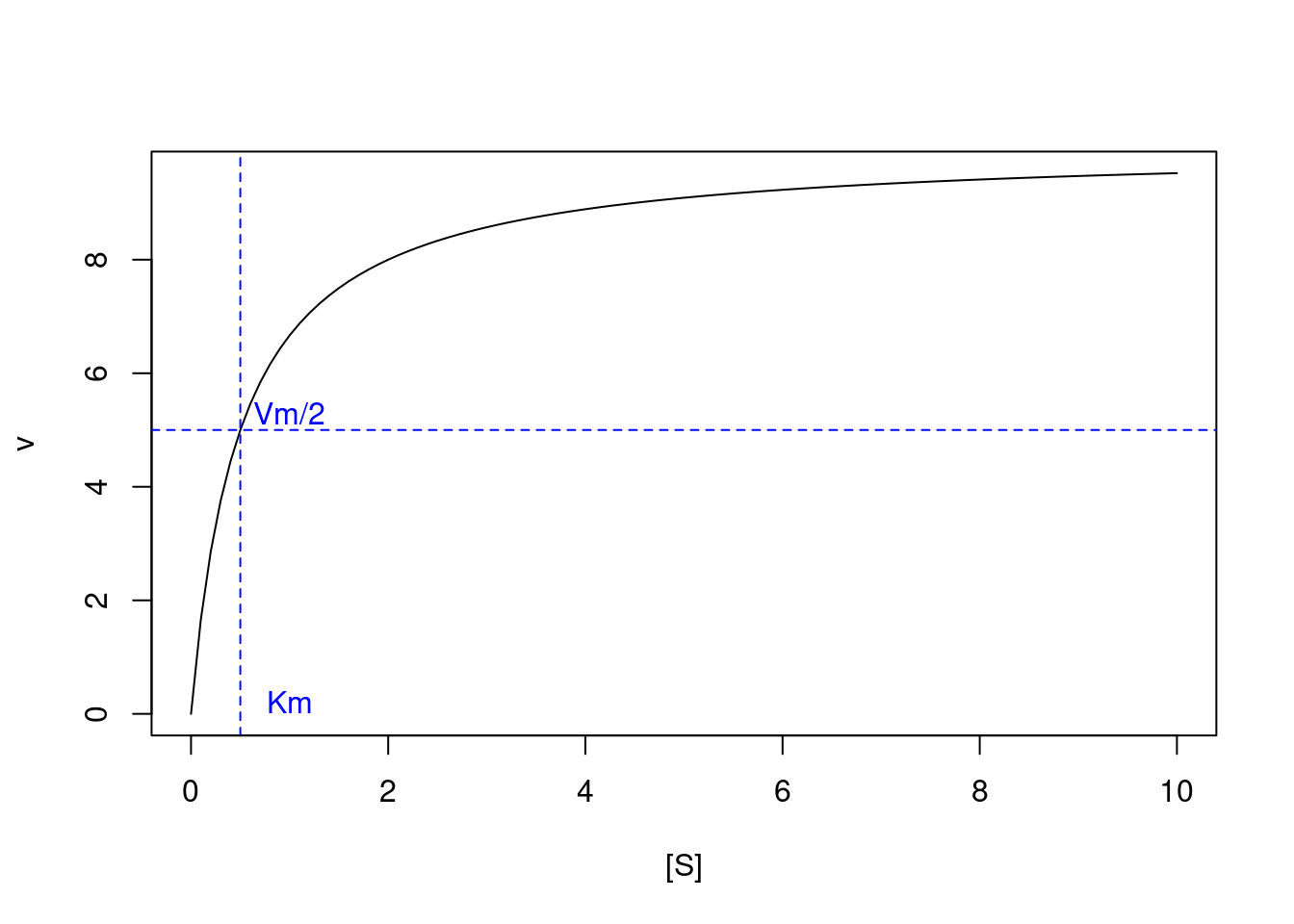

Figura 5.1: Curva de Michaelis-Mentem para uma enzima exibindo Vm=10 e Km=0,5 (50 curvas).

      Por essa relação, o valor de Km é representado pelo teor de substrato que confere metade do valor de Vm para a reação. Observe que pela equação (5.2) o valor de Km no denominador influencia inversamente a velocidade v da reação; ou seja, quanto maior o valor de Km, menor a taxa da reação enzimática. Isto pode ser ilustrado iterativamente com um loop, tal como segue:

Vm=10
Km=seq(from=0.1,to=10,by=0.2) # sequência para 50 valores de Km
for(i in 1:length(Km)) { # loop para adicionar curva de Michaelis-Mentem a cada valor de Km
  add<-if(i == 1) FALSE else TRUE # controle de fluxo que permite adição de curva a partir da segunda iteração (ou seja, quando i > 1)
curve(Vm*x/(Km[i]+x), col= i, lwd=0.8, from =0, to=10, n =100,
      xlab="[S}", ylab="v", add=add)
} 
arrows(0.5,9,3,6,length=0.1,angle=45, col="blue") # seta para Km
text(0.2,9,"Km",col="blue") # indexador para Km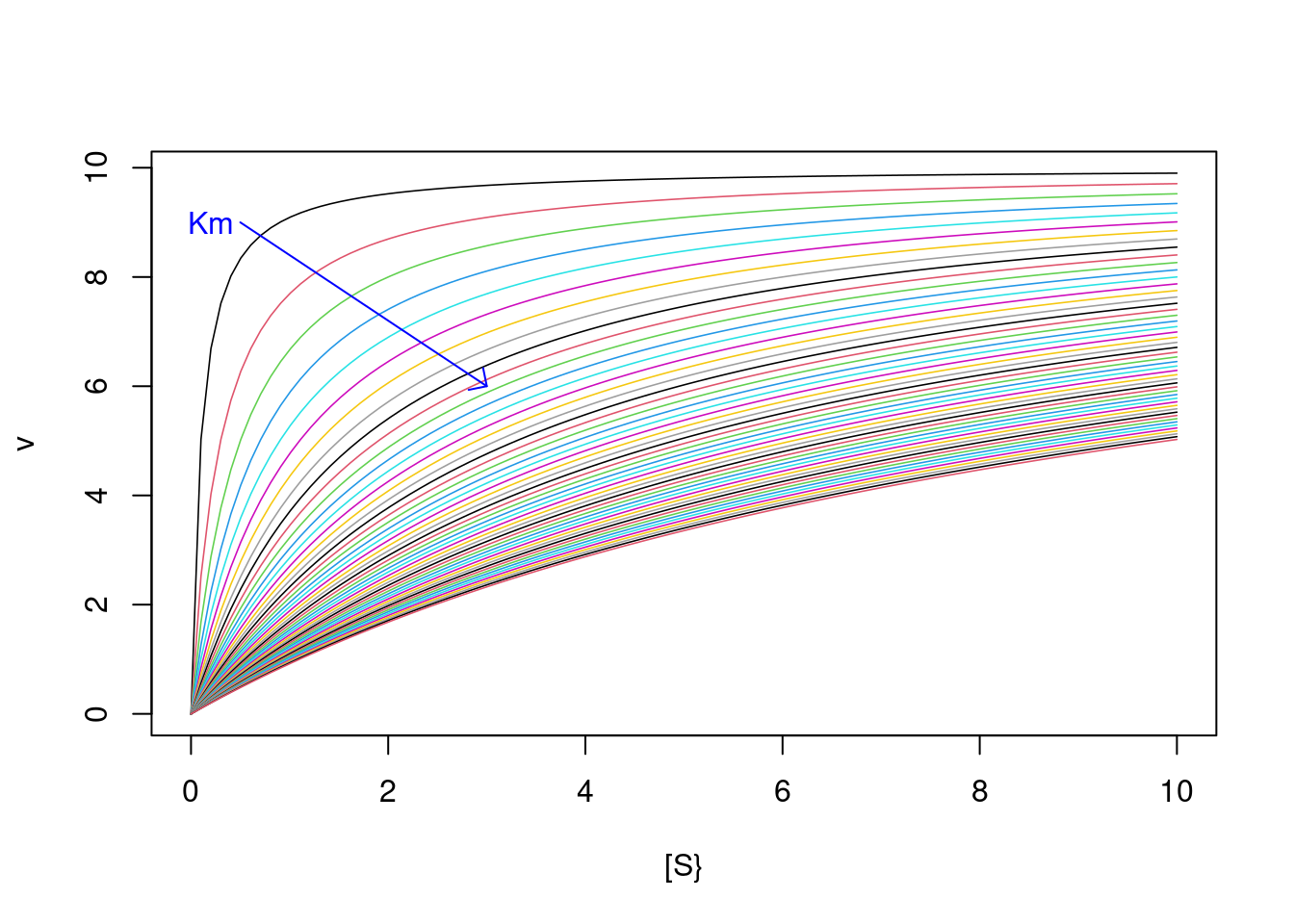

Figura 5.2: Curvas de Michaelis-Menten com variação iterativa para Km de 0.1 a 10.

      As curvas representadas nas figuras 5.1 e 5.2 foram produzidas com a equação (5.2), sendo possível extrair os parâmetros cinéticos Vm e Km facilmente, já que não há desvios computados para a velocidade inicial da reação. Se, por outro lado, estivermos diante de valores experimentais de uma catálise de comportamento de michaelinano e desejarmos extrair os parâmetros cinéticos, melhor será ajustar a equação não-linear de Michaelis-Menten diretamente (algoritmos como Gauss-Newton, Simplex, Levenberg-Marquadt) ou, de modo mais simples, transformar as variáveis S e v de tal modo que permitam um ajuste linear por mínimos quadrados.
      Não obstante, a equação que descreve a equação de Michaelis-Mentem constitui uma hipérbole quadrática e, como tal, não possui assíntota matemática, apenas visual. De fato, os próprios autores do trabalho original, Leonor Michaelis e Maud Mentem, reportaram seus dados com a representação de S em eixo logaritmo permitindo melhor visualização da região assintótica do gráfico (Michaelis and Menten 1913).

5.1 Obtenção de parâmetros cinéticos a partir de dados expermentais simulados

      Para a determinação dos parâmetros cinéticos Vm e Km obtidos a partir de uma simulação experimental de dados de S e v, é necessário em primeiro lugar obter-se os pontos experimentais, tal como segue:

Vm=10
Km=0.5
set.seed(1500) # fixa a semente para geração de dados aleatórios reproduzíveis
erro=runif(20,0,1) # comando para erro uniforme (no. de pontos, min, max)
curve(Vm*x/(Km+x)+erro, type="p", from =0, to=1, n =20,
      xlab="[S}", ylab="v") # elaboração da curva com cômputo de erro uniforme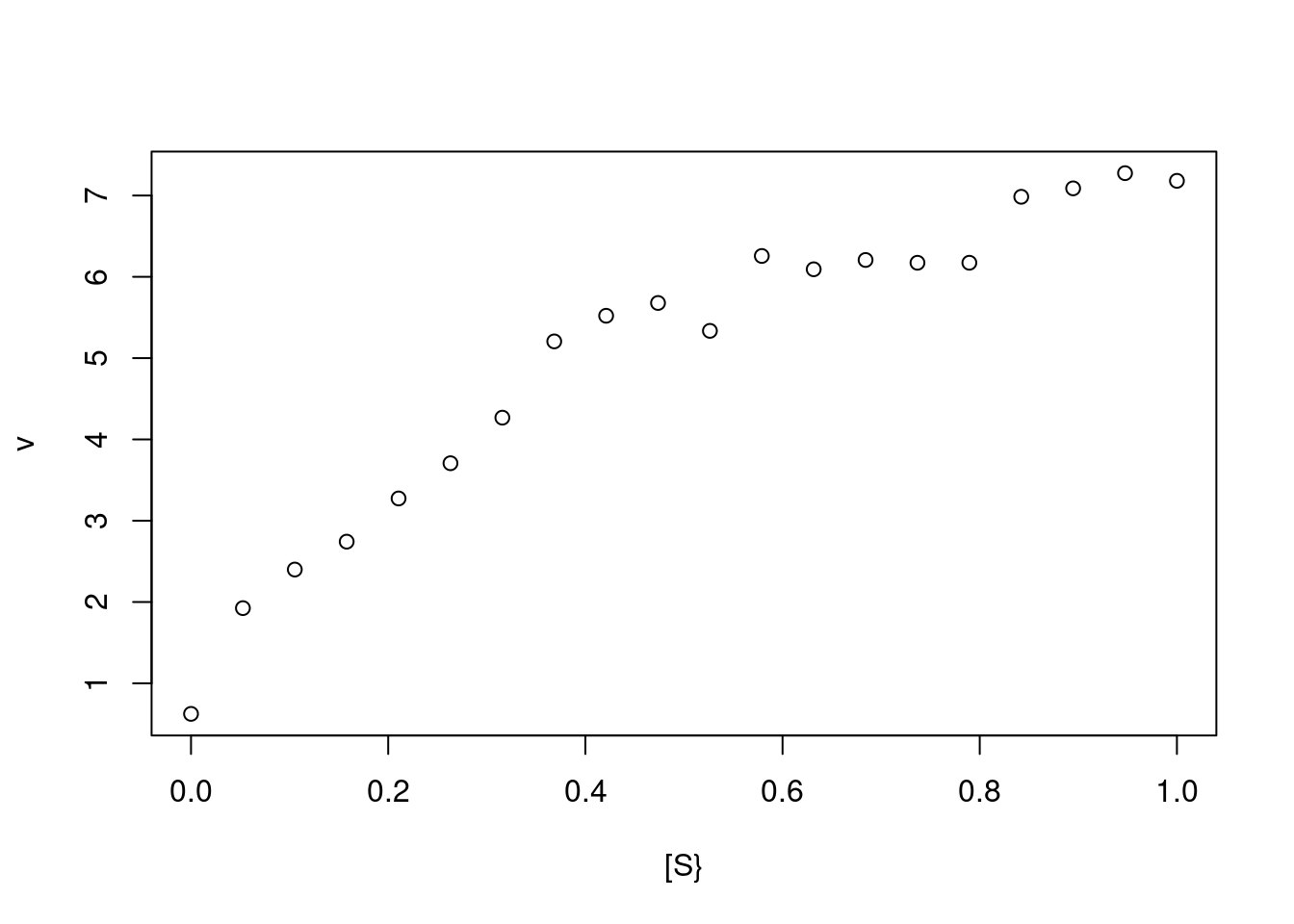

Figura 5.3: Simulação de pontos experimentais (n=20) obtidos a partir da equação de Michaelis-Menten.

      Perceba que pela figura 5.3, já não é mais possível definir-se uma região assintótica que permita a determinação de Vm e, por consequência, de Km. Nesse caso, pode-se obter os parâmetros cinéticos por tranformação da função hiperbólica de Michaelis-Mentem para uma função linear correlata, sucedendo-se o ajuste linear dos dados transformados para a obtenção dos parâmetros de catálise.

5.2 Linearizações e ajustes

      Diversas são as linearizações encontradas na literatura para a equação de Michaelis-Mentem. Para exemplificá-las, segue um trecho de código contendo as quatro mais empregadas. Para isso utilizou-se um par de funções do R para, respectivamente, estabelecer a área gráfica e sua subdivisão para plotagem em 4 paineis (par e mfrow ou mfcol):

S=c(0.1,0.2,0.5,1,5,10,20) # cria um vetor para substrato
Km=0.5;Vm=10 # estabelece os parâmetros enzimáticos
v=Vm*S/(Km+S) # aplica a equação de MM ao vetor de S
par(mfrow=c(2,2)) # estabelece área de plot pra 4 gráficos
plot(S,v,type="o",main="Michaelis-Mentem")
plot(1/S,1/v,type="o",main="Lineweaver-Burk")
plot(v,v/S,type="o",main="Eadie-Hofstee")
plot(S,S/v,type="o",main="Hanes-Woolf")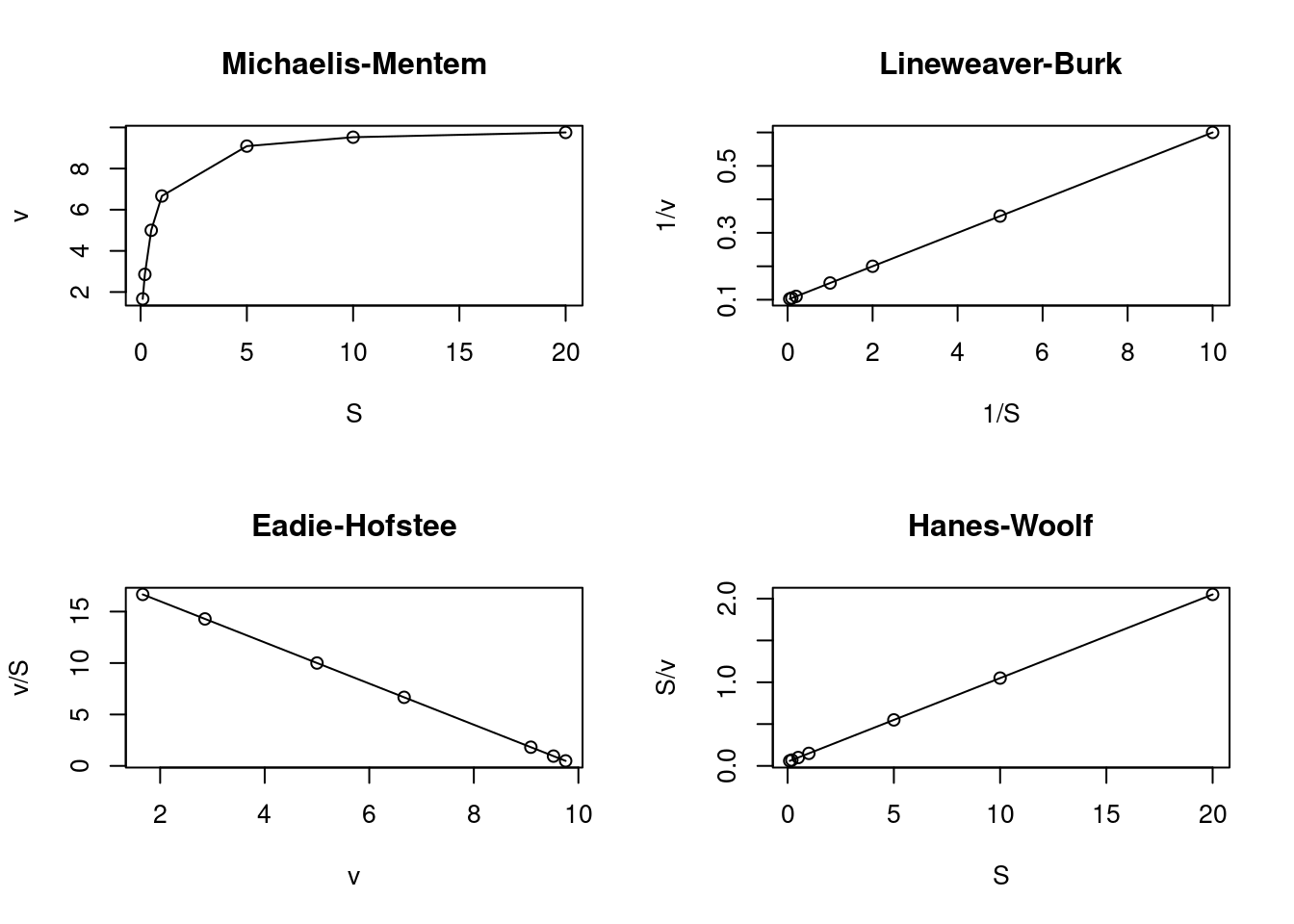

Figura 5.4: Principais linearizações da equação de Michaelis-Menten.

layout(1) # volta à janela gráfica normal

      Dentre essas transformações lineares para cinética enzimática, as mais frequentemente encontradas são de Lineweaver-Burk (ou duplo-recíproco), e a de Eadie-Hofstee, sendo a primeira a mais comum na literatura. No entanto, a aplicação do formalismo de Eadie-Hofstee para interação ligante-proteína também é a mais reportada nessa área, embora seja tratada como representação de Scatchard (Scatchard 1949).

5.2.1 Linearização por transformação de Lineweaver-Burk

      A forma linear para a equação de Linewaver-Burk é obtida a partir da transformação da equação de Michaelis-Menten que segue:

\[\begin{equation} \frac{1}{v}=\frac{1}{Vm}+\frac{Km}{Vm}*\frac{1}{S} \tag{5.3} \end{equation}\]

      Dessa forma, os dados obtidos pela figura 5.3 são transformados para seu duplo-recíproco, resultando em:

S=seq(0.1,1,length.out=20) # gera uma sequência com 20 pontos entre 0 e 1 para valores de substrato
Vm=10; Km=0.5 # parâmetros cinéticos
set.seed(1500) # estabelecer a mesma semente aleatória do gráfico direto de Michaelis-Menten, para reproducibilidade dos pontos
erro=runif(20,0,1) # comando para erro uniforme (no. de pontos, min, max)
v=Vm*S/(Km+S)+erro # equação de Michaelis-Menten

inv.S=1/S # cria variáveis para o duplo-recíproco
inv.v=1/v
plot(inv.v~inv.S, xlab="1/S", ylab="1/v") # elabora o gráfico de Lineweaver-Burk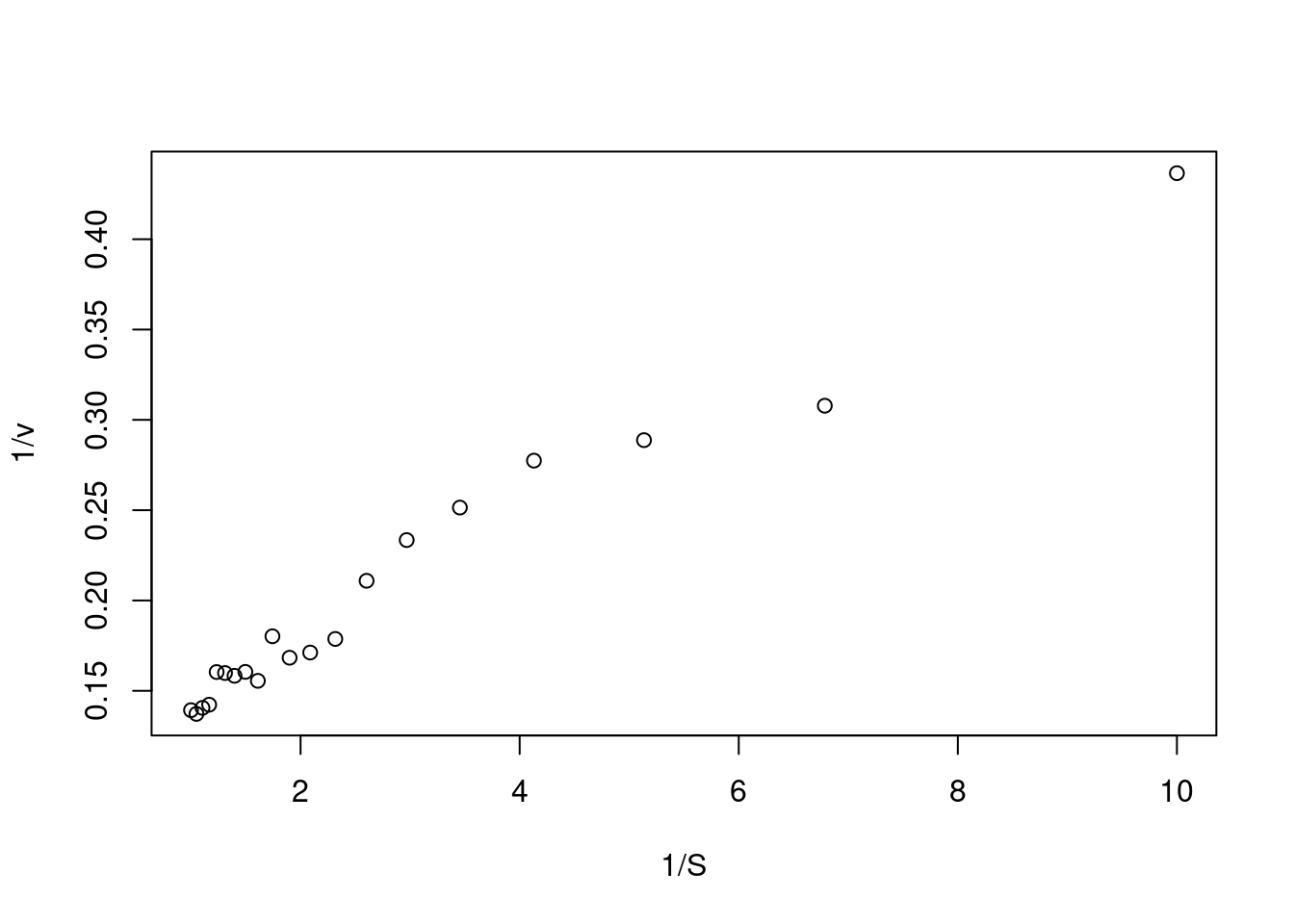

Figura 5.5: Representação de Lineweaver-Burk para os dados simulados da curva de Michaelis-Menten.

      Observe que a figura 5.5 apresenta agora um uma distribuição de valores que possibilita seu ajuste linear por mínimos quadrados (regressão linear). No R, isso pode ser facilmente conduzido pelo trecho de código (chunk) que segue:

reg.LB<-lm(inv.v~inv.S) # expressão para ajuste linear
summary(reg.LB) # resultados do ajuste

## 
## Call:
## lm(formula = inv.v ~ inv.S)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.02820 -0.00986 -0.00350  0.00748  0.02842 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.11363    0.00515    22.1  1.7e-14 ***
## inv.S        0.03277    0.00146    22.4  1.3e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01 on 18 degrees of freedom
## Multiple R-squared:  0.965,  Adjusted R-squared:  0.964 
## F-statistic:  503 on 1 and 18 DF,  p-value: 1.33e-14

plot(inv.v~inv.S, xlab="1/S", ylab="1/v") # gráfico de Lineweaver-Burk
abline(reg.LB, col="blue") # sobreposição do ajuste ao gráfico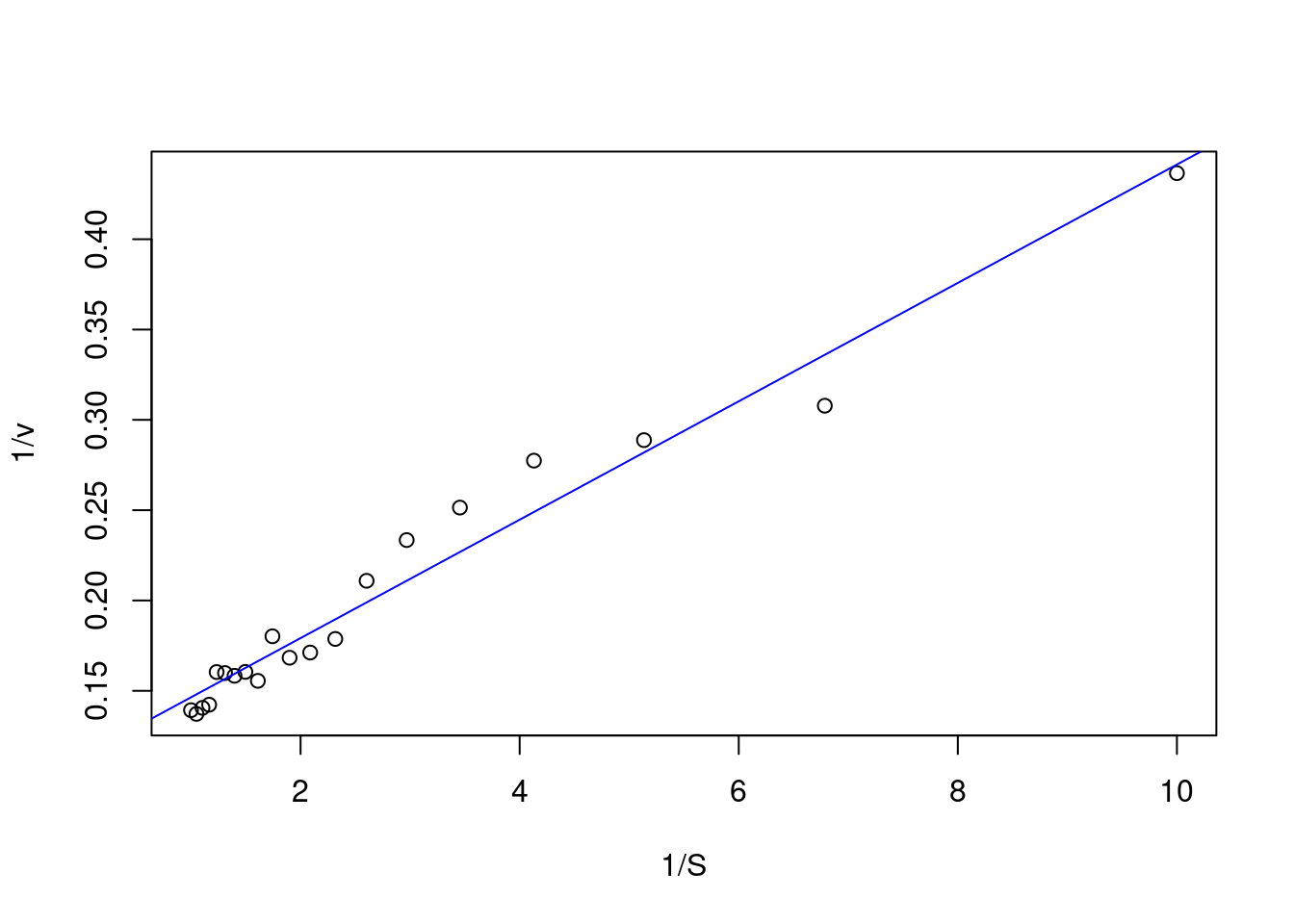

Figura 5.6: Ajuste linear para os dados de Lineweaver-Burk.

      A tabela produzida pelo R para a função lm de ajuste linear por mínimos quadrados possui diversas informações que nos permite avaliar a qualidade da regressão. Brevemente, esse tabela nos fornece o valor de cada parâmetro do ajuste conforme a equação que segue:

\[\begin{equation} y = a + b *x \tag{5.4} \end{equation}\]

      Nesse caso, a refere-se ao intercepto presente na tabela ((intercept), ou 1/Vm) e b à inclinação (inv.S, ou Km/Vm). Além disso, a tabela também fornece diversos resultados complentares, elencados a seguir:

1. valor de erro-padrão dos parâmetros (Std. Error);

2. valor da distribuição t de Student (t value);

3. o respectivo nível de probabilidade (Pr) com indicação de significância (asteriscos);

4. erro padrão residual (Residual standard error);

5. valor dos coeficientes de determinação bruto (Multiple R-squared) e ajustado para os graus de liberdade (Adjusted R-squared);

6. valor da distribuição F de Snedocor (F-statistic) de variância do ajuste;

7. graus de liberdade (DF) e o valor de significância da regressão ao modelo linear obtido pela análise de variância (p-value).

      Não obstante, a qualidade do ajuste linear também pode ser verificada pela produção de gráficos diagnósticos estatísticos, bastando-se aplicar o trecho simples abaixo:

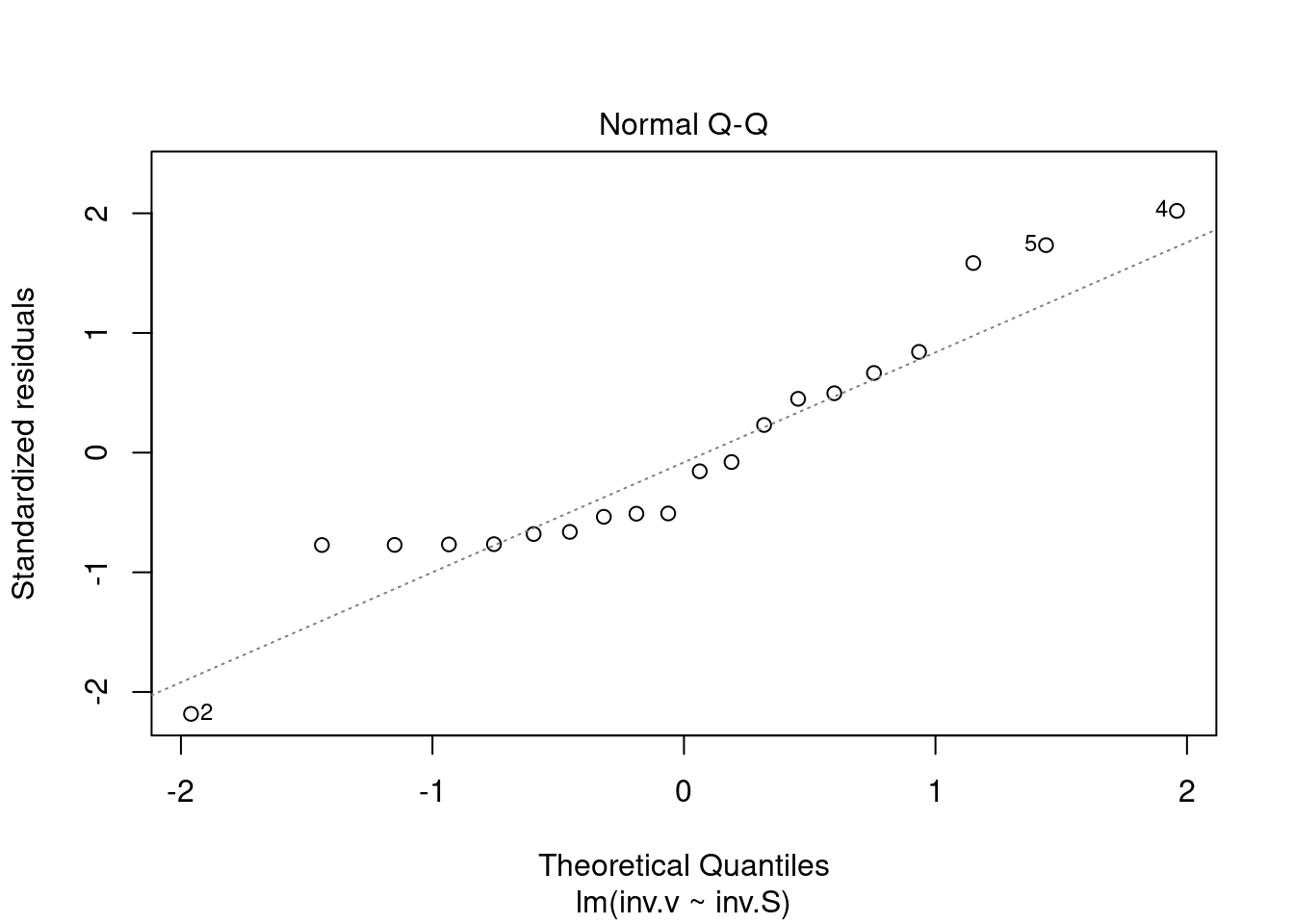
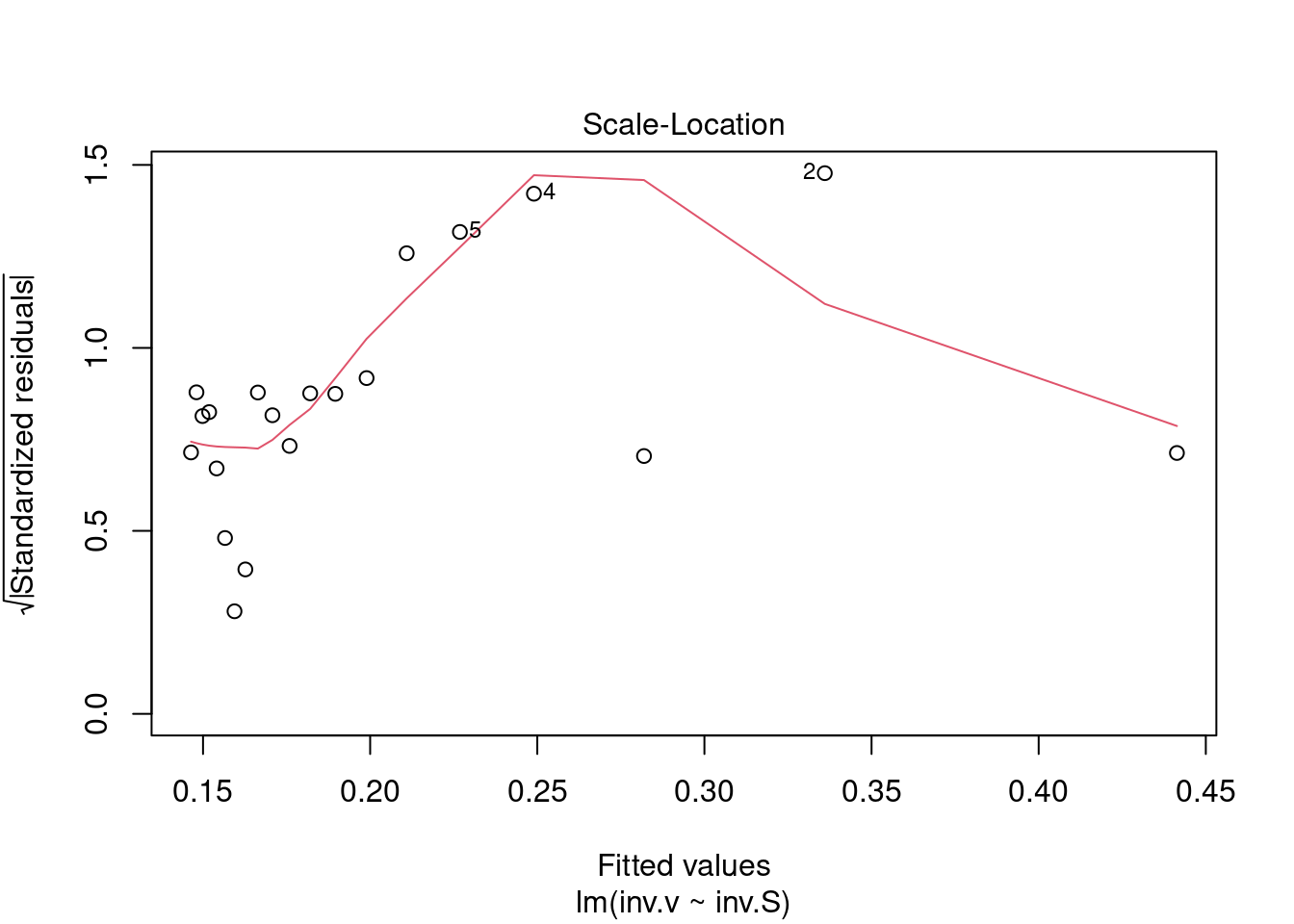
plot(reg.LB) # comando para geração de gráficos diagnósticos de ajuste linear

      Esses gráficos diagnósticos também podem ser alocados em paineis, como ilustrado para as linearizações de Michaelis-Mentem acima.

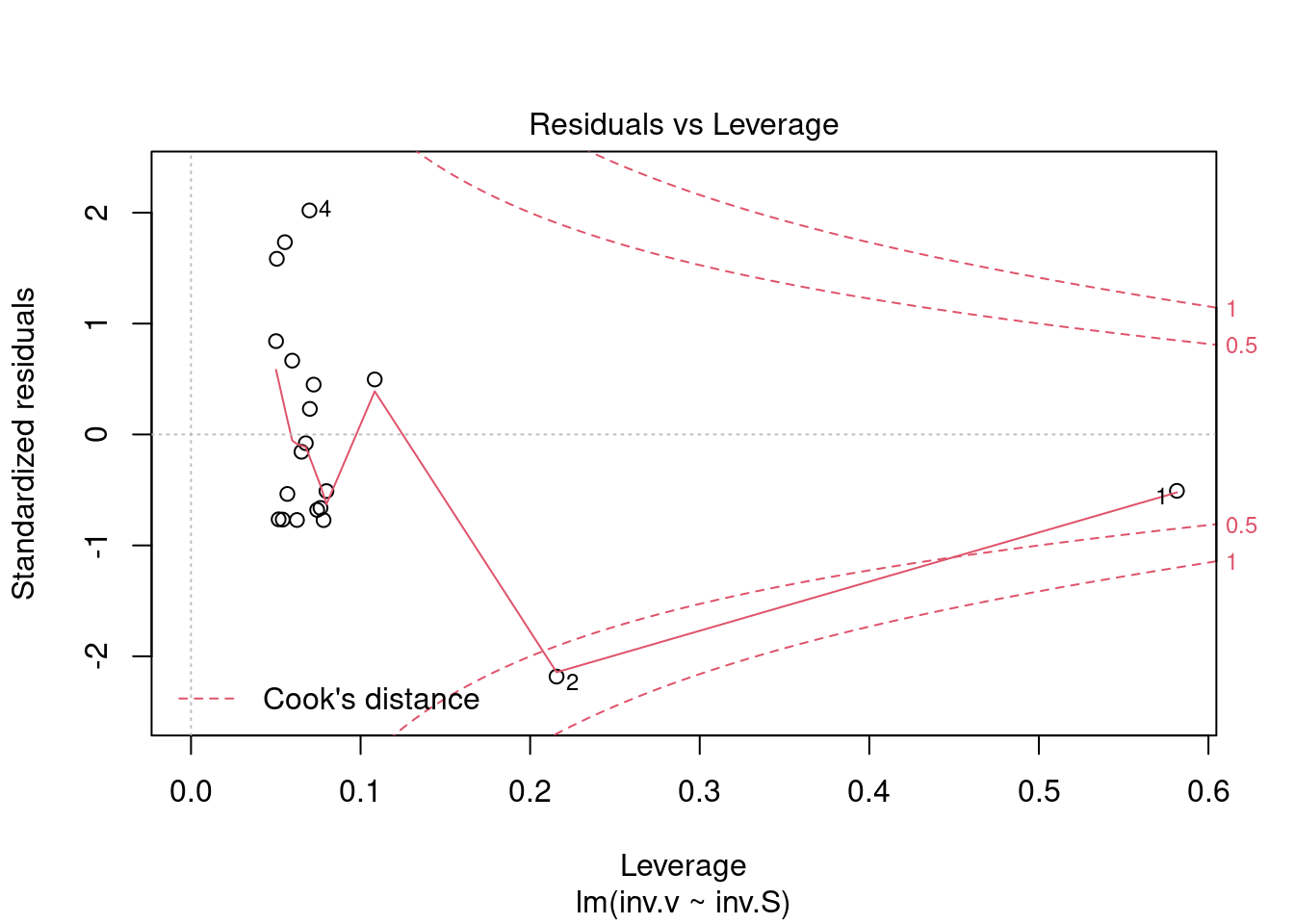
reg.LB<-lm(inv.v~inv.S)
par(mfrow = c(2, 2))
plot(reg.LB)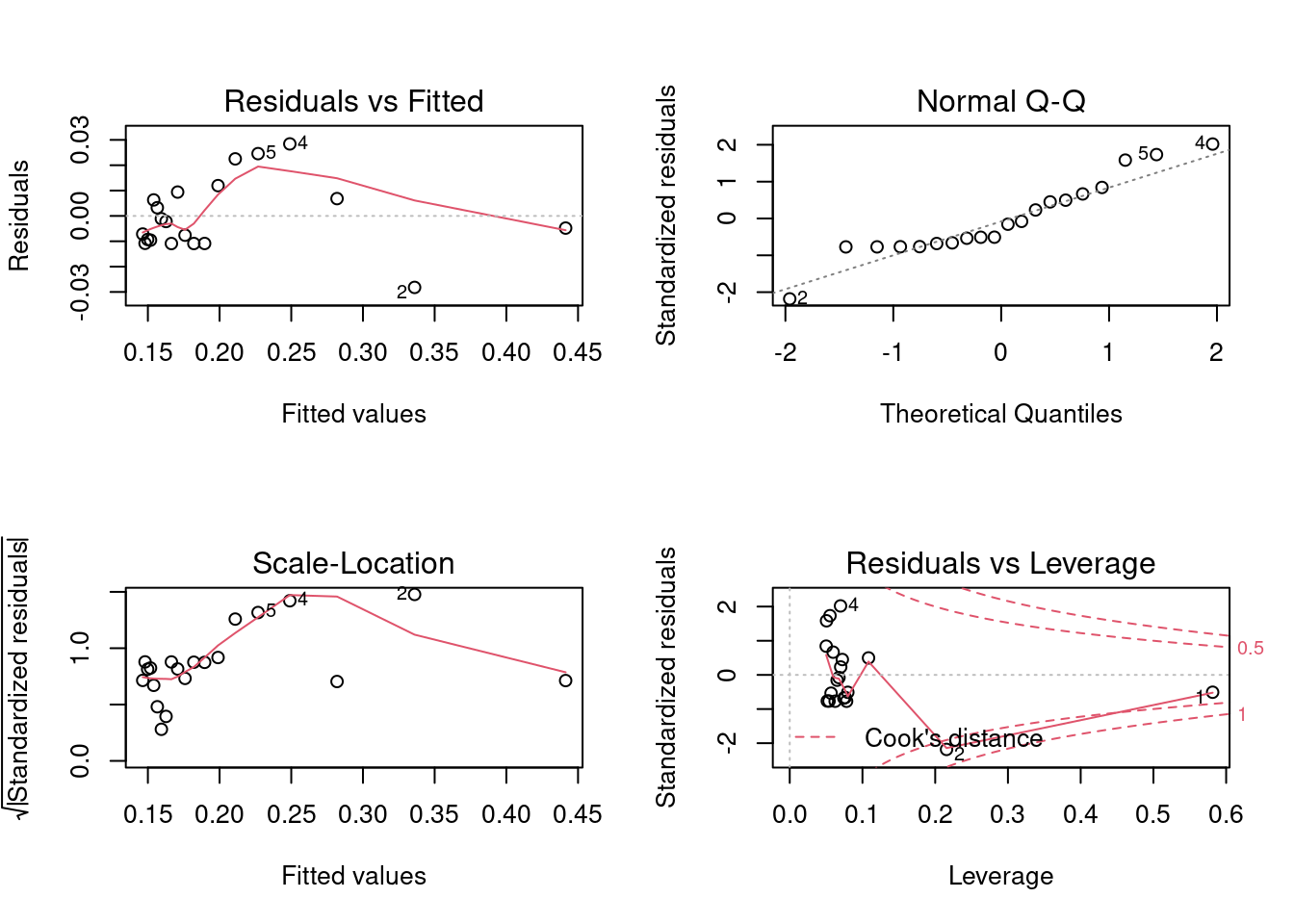

Figura 5.7: Gráficos diagnósticos de ajuste linear.

layout(1)

      Os quatro gráficos gerados acima referem-se, respectivamente, 1) à variação de resíduos com os valores ajustados, 2) a um teste de distribuição normal dos resíduos, 3) à variação de resíduos padronizados em função dos valores ajustados, e 4) à observação de valores influenciáveis identificáveis pela distância de Cook para cada observação. Em relação à esse último, pode-se opcionalmente definir sua aparência para identificação daqueles valores por seleção (which, 4 ou 6, por ex), tal como em:

plot(reg.LB, which = 4)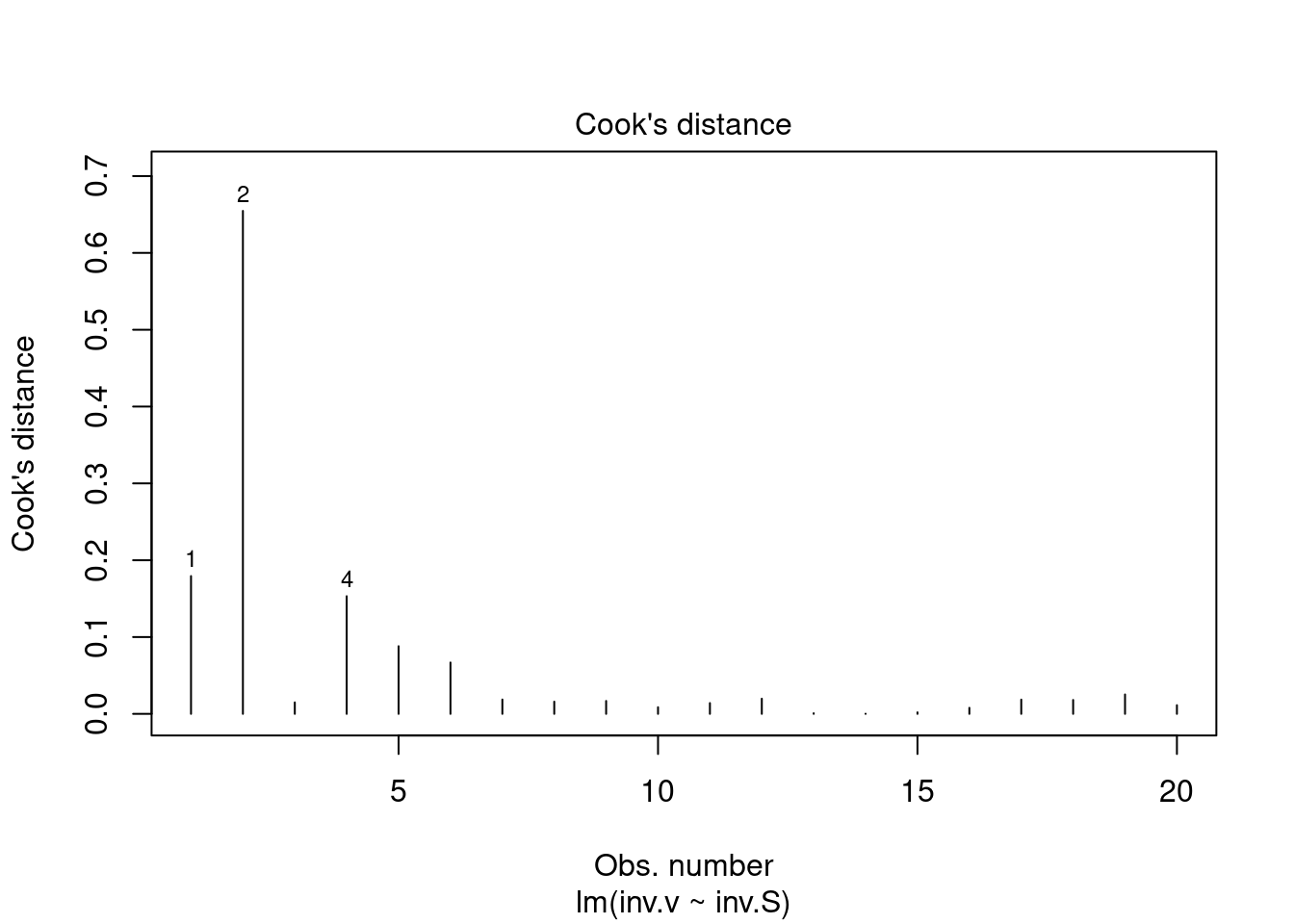

      Por esses dois procedimentos, tabela e gráficos diagnósticos, é possível aferir a qualidade de um ajuste linear pelo R. Em paralelo, diversas são as funções associadas à própria função lm para modelos lineares (objetos), o que reforça o caráter de linguagem orientada a objeto do R. Entre essas vale citar, com significado intuitivo, coef, fitted, predict, residuals, confint, e deviance.
      Para acessar os parâmetros contidos na função lm, assim como outras de mesma natureza no R, basta digitar args:

args(lm)

## function (formula, data, subset, weights, na.action, method = "qr", 
##     model = TRUE, x = FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE, 
##     contrasts = NULL, offset, ...) 
## NULL

      Complementarmente, vale mencionar a existência de inúmeros pacotes do R para diversas situações e tratamentos estatísticos de dados para modelos lineares, e que fogem ao escopo deste manuscrito, tais como os que possibilitam análises de outliers (valores extremos), Generalized Linear Models, Mixed Effects Models, Non-parametric Regression, entre outros. Entre os pacotes do R complementares para regressão linear vale mencionar car, MASS, caret, glmnet, sgd, BLR, e Lars.

5.2.1.1 Considerações sobre a linearização por Lineweaver-Burk.

      De volta ao estudo da cinética de estado estacionário da catálise enzimática, mencionamos acima a possibilidade de linearizações da equação de Michaelis-Mentem por dois tratamentos mais comuns, Lineweaver-Burk e Eadie-Hofstee. De modo geral, qualquer tratamento que resulte na transformação de um modelo original (equação de Michaelis-Menten, no caso) por linearização resultará em desvios estatísticos.

      Analisando a equação de Lineweaver-Burk, por exemplo, pode-se evidenciar que, como os valores de S e v estão representados por seus recíprocos, uma pequena variação em v resultará numa grande variação em 1/v. Por outro lado, a escolha da faixa de teores de S também é extremamente importante para a extração de parâmetros cinéticos. Isso pode ser ilustrado no exemplo que segue:

Vm=10; Km=0.5
set.seed(1500) # semente fixa para erro aleatório
erro=runif(length(S),0,0.1)
S=seq(1,10,0.1)
v=Vm*S/(Km+S)+erro

## Warning in Vm * S/(Km + S) + erro: longer object length is not a multiple of
## shorter object length

plot(v~S, xlab="S", ylab="v")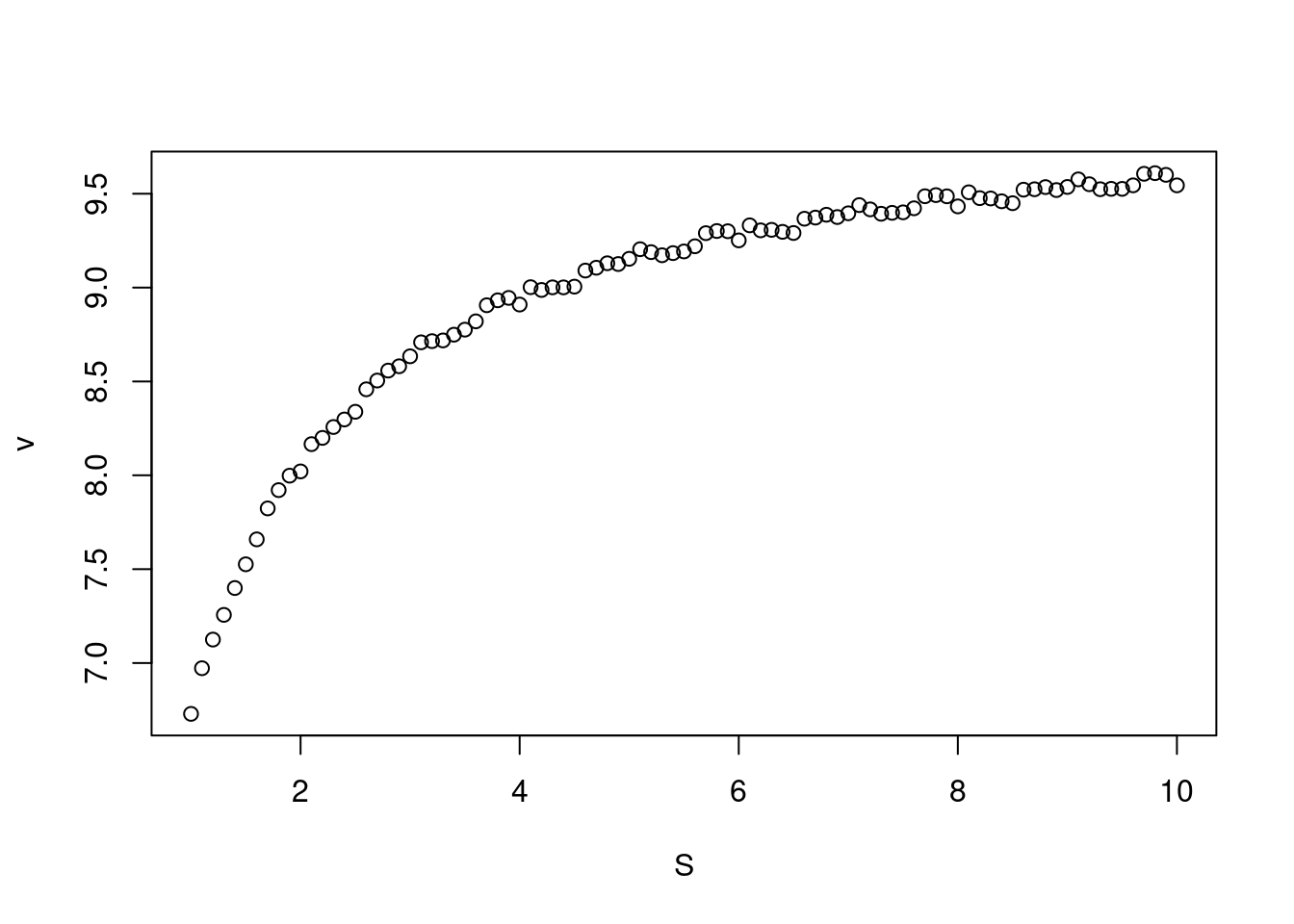

Figura 5.8: Curva de Michaelis-Mentem simulada com erro experimental aleatório. Vm=10; Km=0.5.

      Observe que a figura 5.8 inicia em velocidade próxima a zero, e termina em velocidade próxima à Vm, com teor de S >> Km (50 vezes, de fato). Essa condição permite uma extração segura dos parâmetros cinéticos, os quais podem ser obtidos a partir do ajuste linear do gráfico duplo-recíproco.

set.seed(1500) # semente fixa para erro aleatório
erro=runif(length(S),0,0.2)
Vm=10; Km=0.5 # parâmetros cinéticos
inv.S=1/seq(1,10,0.1) # 1/S
inv.v=1/(Vm*S/(Km+S)+erro) # 1/v
plot(inv.S,inv.v)
lm.LB2<-lm(inv.v~inv.S) # ajuste linear
summary(lm.LB2) #resultados do ajuste

## 
## Call:
## lm(formula = inv.v ~ inv.S)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.001505 -0.000561 -0.000146  0.000752  0.001412 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.099181   0.000136     731   <2e-16 ***
## inv.S       0.048156   0.000419     115   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8e-04 on 89 degrees of freedom
## Multiple R-squared:  0.993,  Adjusted R-squared:  0.993 
## F-statistic: 1.32e+04 on 1 and 89 DF,  p-value: <2e-16

abline(lm.LB2, col="blue")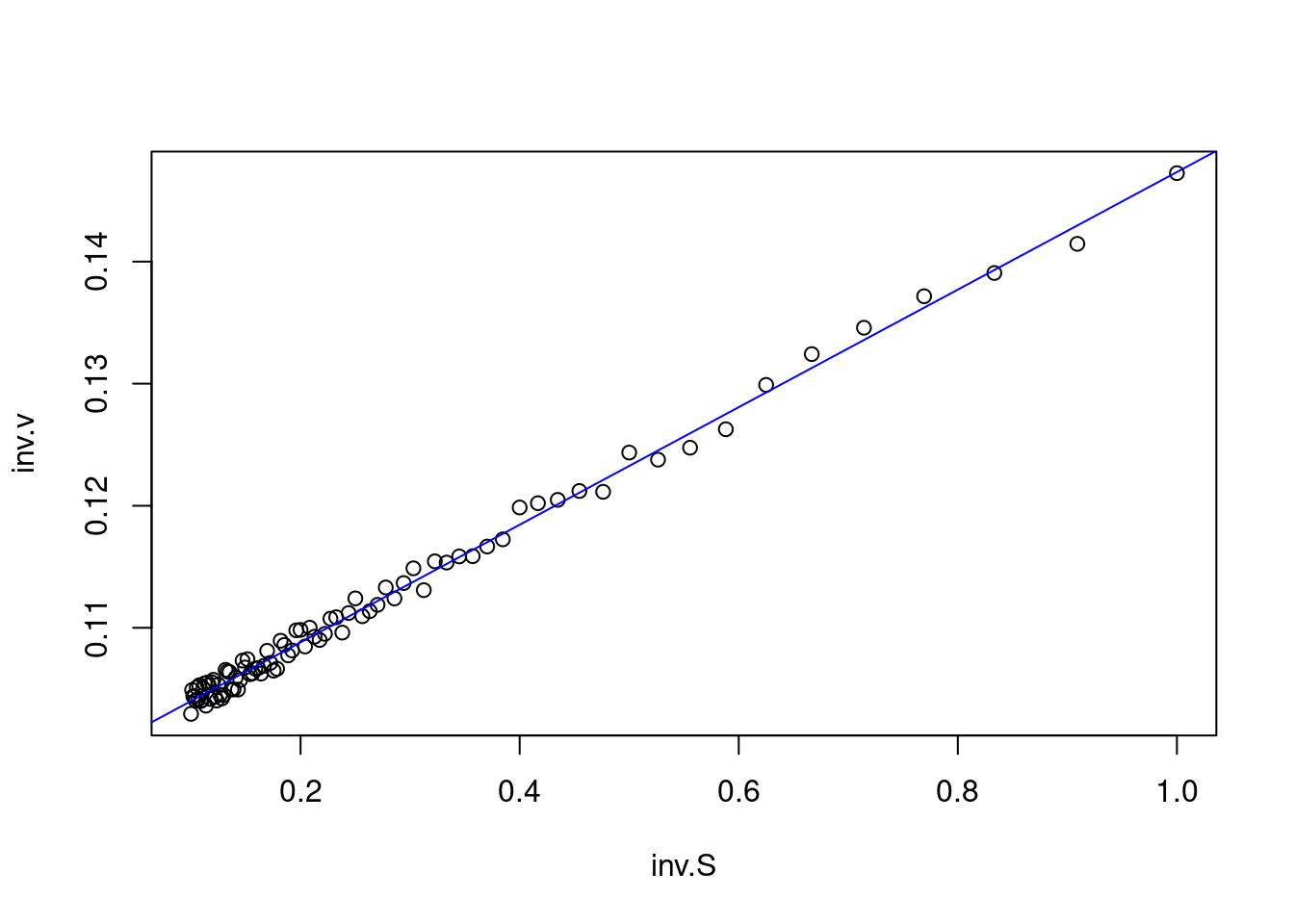

Figura 5.9: Lineweaver-Burk dos dados do gráfico anterior.

      Perceba como os valores de Vm e Km ajustados aproximaram-se dos valores preditos, já que para o gráfico duplo-recíproco:

\[\begin{equation} Vm=1/intercepto \\ Km = intercepto * Vm \tag{5.5} \end{equation}\]

      Agora, o que aconteceria se os pontos experimentais estivessem em faixas distintas de teores de S ? Exemplificando, se os pontos fossem coletados em três regiões distintas de S: 10-100, 30-100, e 50-100 ?

Isso pode ser ilustrado variando-se a faixa de valores de S iterativamente, e inspecionando-se o gráfico duplo-recíproco resultante como no trecho de código que segue, e para os mesmos valores da figura 5.9.

set.seed(1500) # mesma semente aleatória para reproducibilidade de erro
Vm=10; Km=0.5 # estabelece os parâmetros de MM
S=seq(10,100,10) # cria-se uma sequência inicial para S
v=Vm*S/(Km+S) # aplicação equação de MM à S
plot(1/S,1/v, type="n",ylim=c(0.098,0.106)) # elabora o duplo-recíproco sem pontos
 for(i in 1:3) { # inicia a iteração para gráficos de Lineweaver-Burk
   S=seq(10*i,100,length.out=100) # gera uma sequência S com 100 pontos, produzindo 5 vetores que iniciam em valores diferentes para S (10, 30 e 50)
   erro=runif(length(S),0,0.1) #  erro para adição à vetor de velocidade inicial, com no. de pontos em função do vetor de S
    add<-if(i == 1) FALSE else TRUE # controle de fluxo para plotagem de pontos no gráfico vazio
    inv.S=1/S; inv.v=1/((Vm*S/(Km+S))+erro)  # novos valores para o duplo-recíproco em função da iteração
 points(inv.v~inv.S, xlab="1/S", ylab="1/v", col=i, add=add) # adição de pontos ao gráfico de Lineweaver-Burk, com identificação por cores (1, 2, 3, 4 e 5)
 lm.LB<-lm(inv.v~inv.S) # elabora o ajuste linear
 abline(lm.LB, col=i, lty=i) # sobrepõe as linhas de ajuste
 }

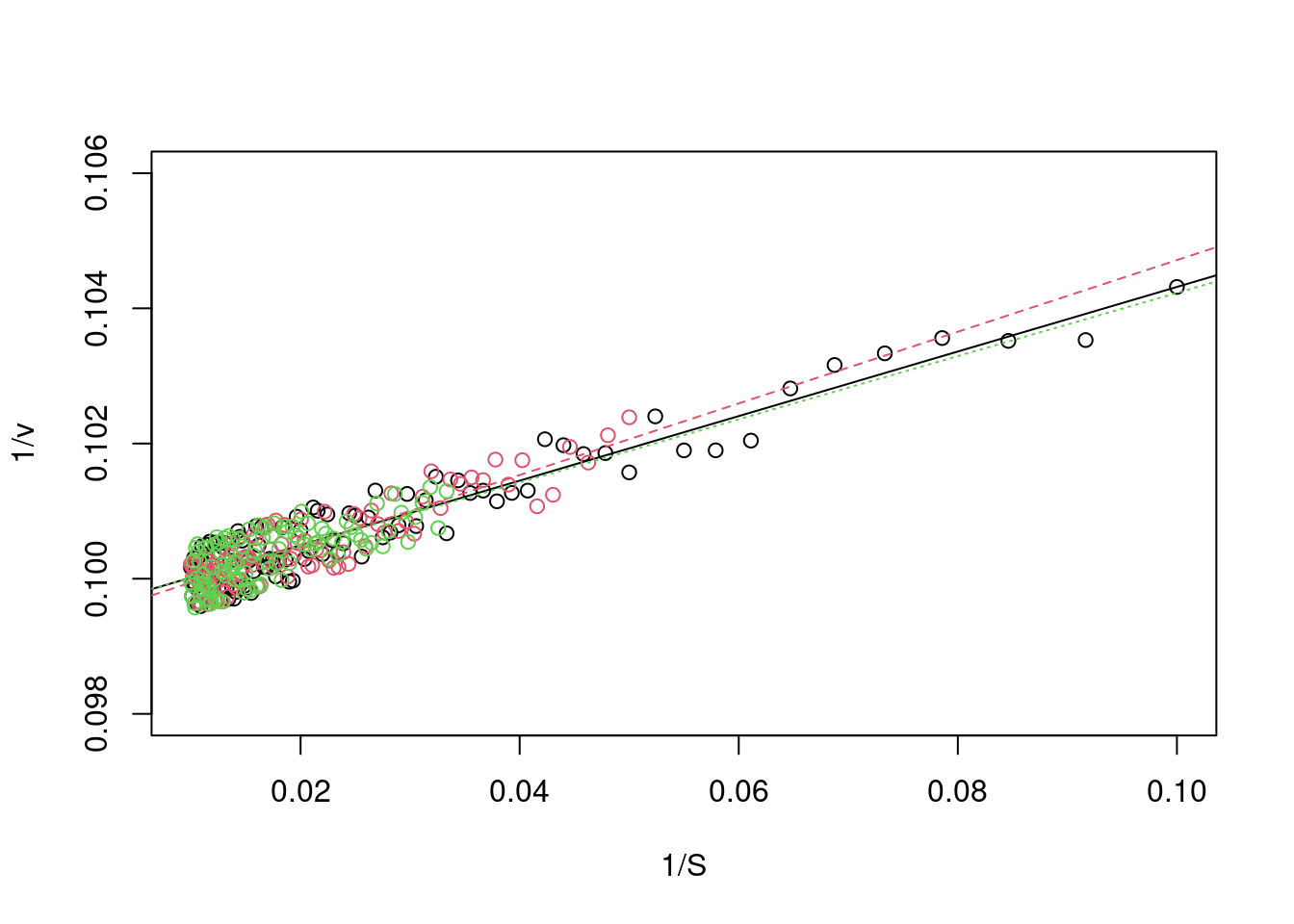
Figura 5.10: Gráficos duplo-recíproco para a curva simulada de Michaelis-Menten, para distintos teores de S inicial.

      Observe agora que pela figura 5.10 resultante, tanto o intercepto como a inclinação obtidos a partir dos ajustes foram dependentes da faixa de seleção de S, o que resulta em distintos valores para Vm e Km. Isto mostra como a seleção da faixa de S para o cálculo de Km e Vm é crucial.

5.2.2 Linearização por transformação de Eadie-Hofstee

      Como já mencionado, as duas linearizações da equação de Michaelis-Menten mais comuns referem-se à do subtítulo acima. A equação de linearização de Eadie-Hosftee é dada abaixo:

\[\begin{equation} v = \frac{1}{Km} * \frac{v}{S} + Vm \tag{5.6} \end{equation}\]

      A partir dos dados da figura 5.3 obtém-se os parâmetros cinéticos diretamente do intercepto (Vm) e da inclinação linear (1/Km) por:

Vm=10; Km=0.5
set.seed(1500) # semente fixa para erro aleatório
erro=runif(length(S),0,0.1)
S=seq(1,10,0.1)
v=Vm*S/(Km+S)+erro
v.S=v/S
plot(v.S~v, xlab="v", ylab="v/S")

lm_EH<-lm(v.S~v); summary(lm_EH)

## 
## Call:
## lm(formula = v.S ~ v)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1160 -0.0650  0.0117  0.0546  0.1248 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 20.31073    0.07906     257   <2e-16 ***
## v           -2.02191    0.00893    -226   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.07 on 98 degrees of freedom
## Multiple R-squared:  0.998,  Adjusted R-squared:  0.998 
## F-statistic: 5.13e+04 on 1 and 98 DF,  p-value: <2e-16

abline(lm_EH, col="blue")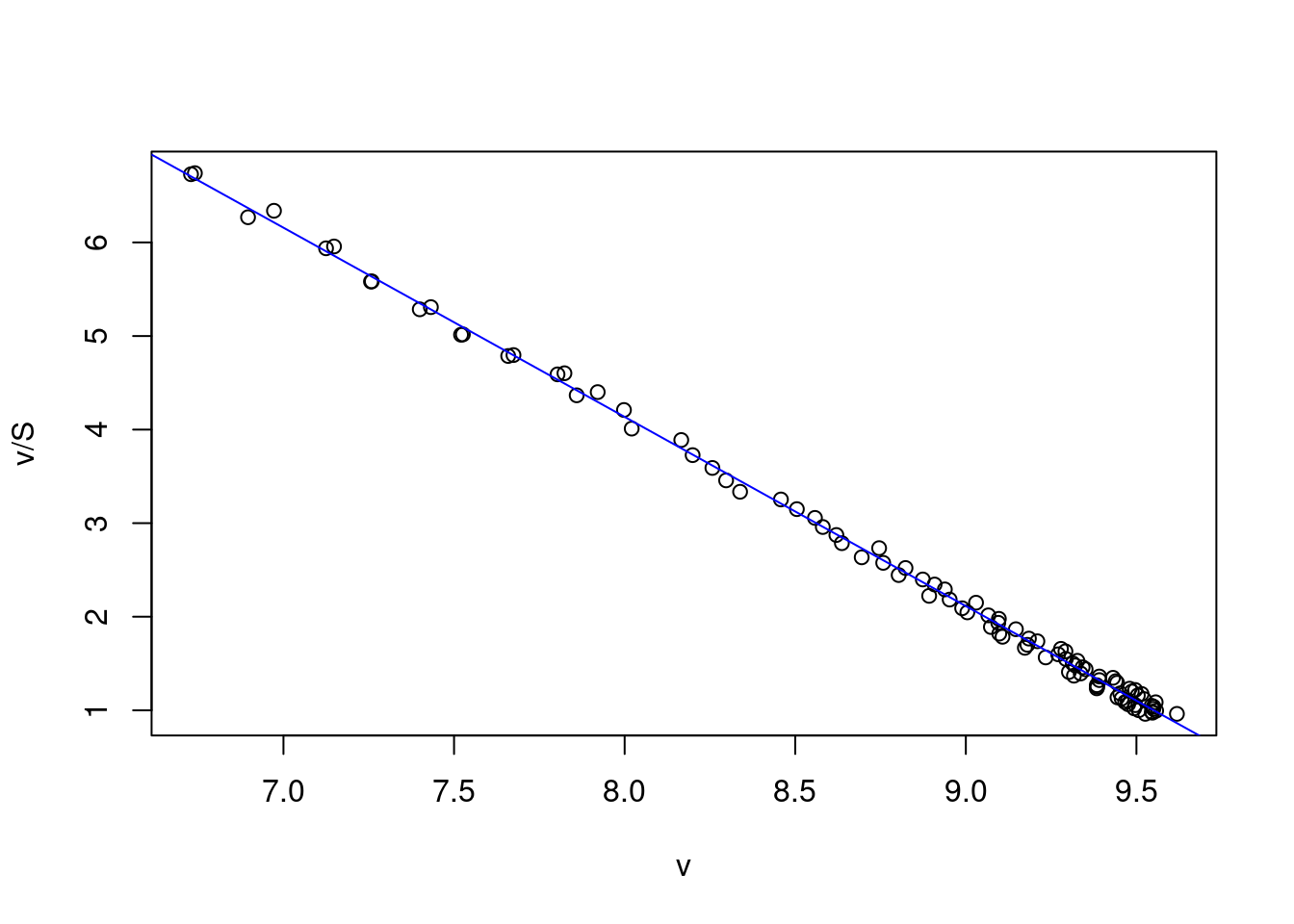

5.2.3 Distribuição de erros nas linearizações de Michaelis-Mentem

      Embora ambas as representações, Lineweaver-Burk e Eadie-Hofstee, sejam as mais utilizadas e apresentem semelhança na obtenção dos parâmetros cinéticos, sua distribuição de resíduos é bem distinta, assim como as demais transformações lineares de Michaelis-Mentem (figura 5.4).
      O código abaixo ilustra a distribuição de erros dessas transformações, introduzindo uma função importante do R para construção de gráficos com barras de erros: arrows.

Vm=10; Km=0.5 # fixa os parâmetros de MM
set.seed(1500) # fixa semente para erro aleatório
erro=runif(length(S),0,0.5) # vetor de erro uniforme
S=c(0.1,0.2,0.5,1,5,10,20) # vetor de substrato
v=Vm*S/(Km+S) # equação de MM
par(mfrow=c(2,2)) # área de plot pra 4 gráficos
plot(S,v,type="o",main="Michaelis-Mentem")
arrows(S,v,S,v-erro,length=.05,angle=90) # barra inferior de erro
arrows(S,v,S,v+erro,length=.05,angle=90) # barra superior de erro

plot(1/S,1/v,type="o",main="Lineweaver-Burk")
arrows(1/S,1/v,1/S,1/(v-erro),length=.05,angle=90)
arrows(1/S,1/v,1/S,1/(v+erro),length=.05,angle=90)

plot(v,v/S,type="o",main="Eadie-Hofstee")
arrows(v,v/S,v,(v-erro)/S,length=.05,angle=90)
arrows(v,v/S,v,(v+erro)/S,length=.05,angle=90)

plot(S,S/v,type="o",main="Hanes-Woolf")
arrows(S,S/v,S,S/(v-erro),length=.05,angle=90)
arrows(S,S/v,S,S/(v+erro),length=.05,angle=90)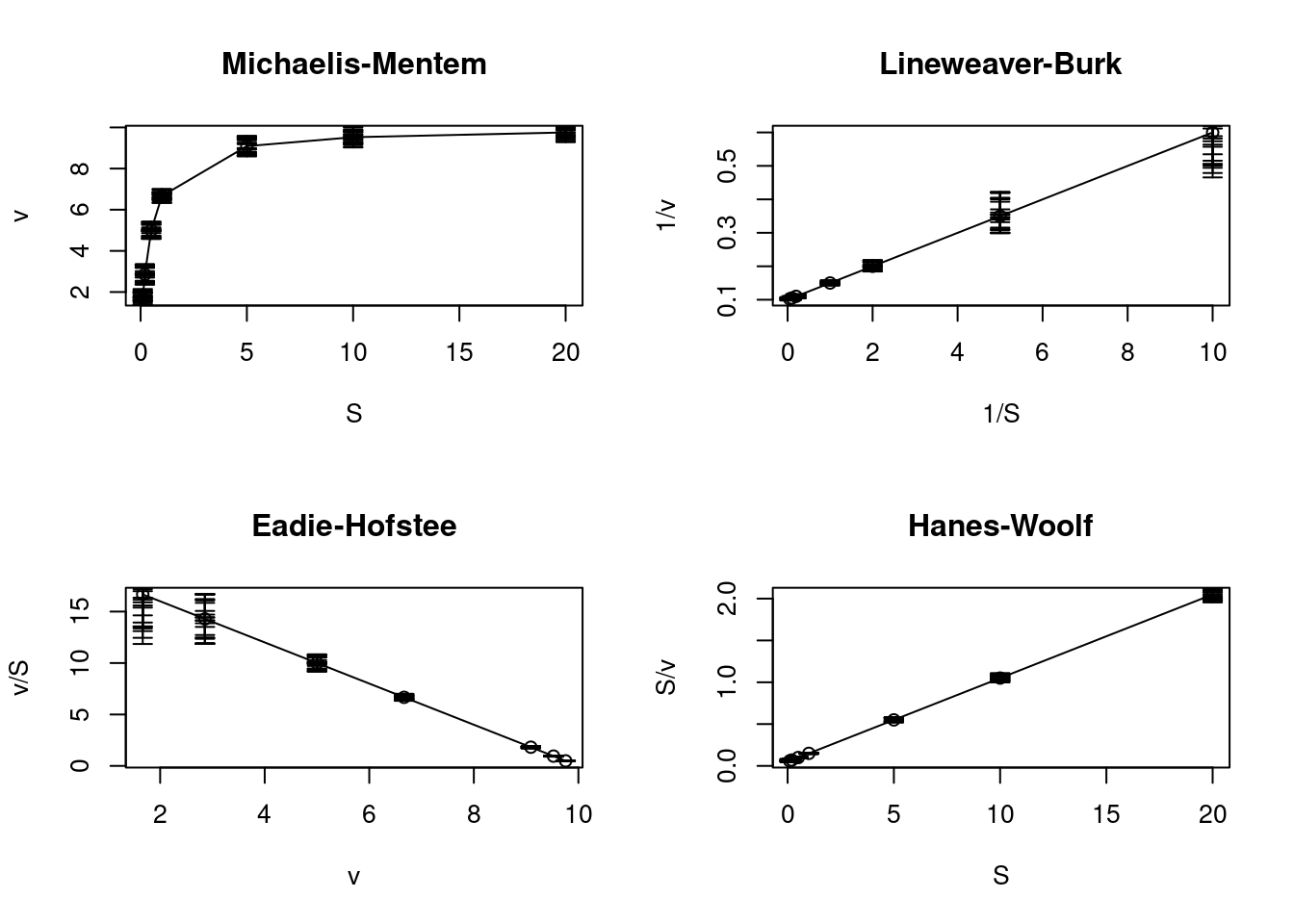

Figura 5.11: Distribuição de erros aleatórios para a equação de Michaelis-Mentem e suas transformações lineares.

par(mfrow=c(1,1)) # retorno à janela gráfica normal

      Pelo gráfico da figura 5.11 fica evidente que as transformações de Lineweaver-Burk e de Eadie-Hofstee, ainda que tenham prevalência na literatura, são as que apresentam a maior variabilidade de erro a partir dos dados experimentais, o que converge para uma menor precisão na determinação de parâmetros cinéticos. Além disso, observa-se que a transformação de Hanes-Woolf é a que apresenta a menor dispersão de resíduos entre as demais, igualando-se aos erros experimentais da equação hiperbólica de Michaelis-Mentem. Apesar disso, a linearização de Hanes-Woolf é muito pouco reportada na literatura.
      Ainda que a representação dos duplos-recíprocos tenha em si algumas desvantagens, tais como a dispersão de erros principalmente em valores baixos de S, é a única dentre as mencionadas que permite um ajuste linear por mínimos quadrados, se considerarmos as premissas estatísticas desse.
      Para que se possa obter parâmetros de intercepto e inclinação a partir de uma regressão linear, é necessário que se cumpra as premissas estatísticas de 1) distribuição normal de resíduos, 2) homogeneidade de variâncias, e 3) independência das variáveis. Se observarmos as três linearizações, tanto a de Eadie-Hofstee como a de Hanes-Woolf não cumprem a premissa de independência, já que a variável dependente (y) é função da independente (x).
      Para que uma transformação por duplos-recíprocos possa ser utilizada mais fielmente à obtenção de parâmetros cinéticos, contudo, pode-se adotar o cômputo de peso na fórmula de ajuste linear, tal como sugerido por Wilkinson (Wilkinson 1961), considerando-o como o recíproco das variâncias estimadas. Nesse caso, o ajuste linear considerando o quadrado do vetor de erros aleatórios como variância e o peso como seu recíproco (1/s²), pode ser esboçado como:

S=seq(0.1,1,length.out=20)
Vm=10; Km=0.5 
set.seed(1500) 
erro=runif(20,0,1)
v=Vm*S/(Km+S)+erro 
inv.S=1/S 
inv.v=1/v
reg.LB.peso<-lm(inv.v~inv.S, weights=1/erro^2) # expressão para ajuste linear
summary(reg.LB.peso) # resultados do ajuste

## 
## Call:
## lm(formula = inv.v ~ inv.S, weights = 1/erro^2)
## 
## Weighted Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.04779 -0.02231 -0.01849  0.00162  0.04830 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.11733    0.00254    46.1  < 2e-16 ***
## inv.S        0.03491    0.00145    24.0  3.9e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03 on 18 degrees of freedom
## Multiple R-squared:  0.97,   Adjusted R-squared:  0.968 
## F-statistic:  578 on 1 and 18 DF,  p-value: 3.93e-15

      Ainda que os ajustes tenham sido realizados para valores com baixa variabilidade de erros uniformes, uma comparação entre esse resultado e o da figura 5.6 revela ligeira superioridade para o primeiro, com maior valor para o coeficiente de determinação R², menor para p-valor, e menores para o erro-padrão das estimativas.
      Complementarmente, pode-se obter uma comparação estatística entre o modelo linear simples e o que adotou o peso estatístico por:

anova(reg.LB,reg.LB.peso)

## Analysis of Variance Table
## 
## Model 1: inv.v ~ inv.S
## Model 2: inv.v ~ inv.S
##   Res.Df     RSS Df Sum of Sq F Pr(>F)
## 1     18 0.00383                      
## 2     18 0.01585  0    -0.012

5.3 Ajuste não-linear

      Ainda que linearizações sejam frequentemente utilizadas mesmo hoje em dia, principalmente para discernir entre modelos cinéticos distintos, a determinação precisa dos parâmetros de catálise é contudo melhor conduzida por ajuste ou regressão não-linear. Esse ajuste tem por objetivo a determinação de parâmetros de uma equação (Vm e Km, no caso) sem a necessidade de qualquer transformação dos dados, eliminando por essa razão os erros associados.
      O ajuste não-linear difere do linear em algumas características, tais como:

1. A busca iterativa de um valor mínimo (local ou global) para a soma dos quadrados dos erros das estimativas;
2. a necessidade de um valor inicial para os parâmetros (sementes);
3. a linearidade nos erros e no gradiente da função sobre os parâmetros.
4. a necessidade de algoritmo mais sofisticado para solução simbólica e matricial para minimizar a derivada da função sobre cada parâmetro;
5. a necessidade de programa que trabalhe com álgebra matricial (computador, dispositivo móvel ou calculadora);
6. o uso de algoritmos mais sofisticados (Gauss, Newton-Raphson, Levenberg-Marquadt, Simplex).
   
7. o emprego da equação original do modelo, por vezes de difícil linearização.

5.3.1 Ajuste não-linear da equação de Michaelis-Mentem

      Para uma regressão não-linear da equação de Michaelis-Mentem reproduzindo-se a simulação exemplificada na figura 5.3:

Vm=10
Km=0.5
set.seed(1500)  
erro=runif(20,0,1) 
S=seq(0,1,length.out=20)
v=Vm*S/(Km+S)+erro
dat.Sv <- data.frame(S,v) # criação de planilha com S e v
plot(v~S, type="p", from = 0, to=1, n = 20,
      xlab="[S}", ylab="v") # construção do gráfico de MM

nl.MM<-nls(v~Vm*S/(Km+S), start = list(Vm=7, Km=0.2), data=dat.Sv) # linha de código para ajuste não linear
lines(S,fitted(nl.MM),col="red") # sobreposição da linha ajustada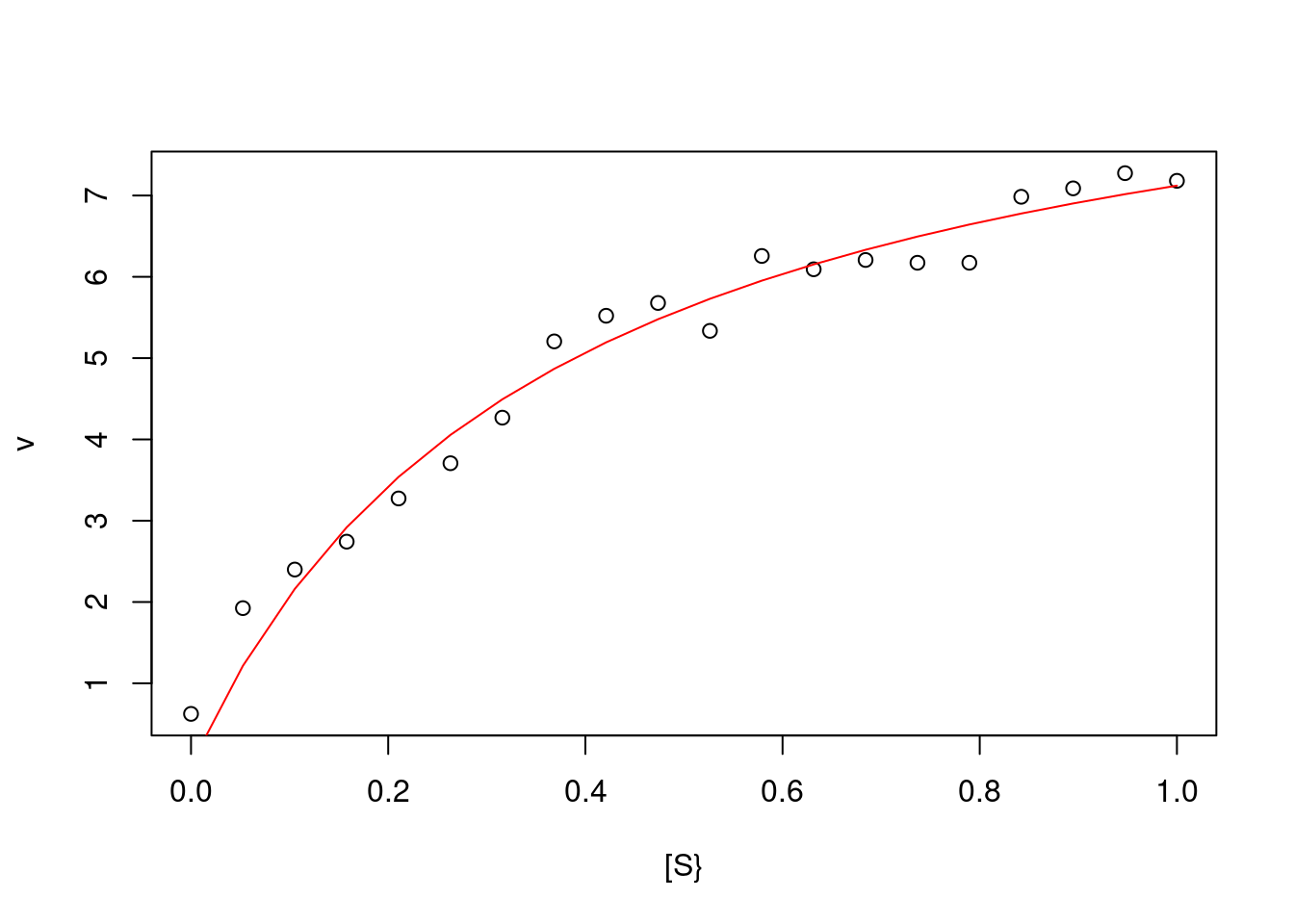

Figura 5.12: Ajuste não linear para a simulação experimental da equação de Michaelis-Menten.

summary(nl.MM) # sumário dos resultados

## 
## Formula: v ~ Vm * S/(Km + S)
## 
## Parameters:
##    Estimate Std. Error t value Pr(>|t|)    
## Vm   9.7549     0.5211   18.72  3.0e-13 ***
## Km   0.3698     0.0502    7.37  7.7e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4 on 18 degrees of freedom
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 1.63e-06

      Observe agora pela tabela de sumário do ajuste que os parâmetros são fornecidos diretamente, sem necessidade de transformação, como no ajuste linear. A tabela diferencia-se do sumário de ajuste linear por apresentar o número de iterações para convergência, e o valor de convergência para tolerância. Contudo, não apresenta o coeficiente de determinação R², mas somente o erro padrão residual. Ainda que a discussão esteja longe da proposta desta obra, alguns autores declinam do emprego de R² em regressão não-linear pelo mesmo ser decorrente de relações lineares entre os parâmetros, o que não ocorre no caso.
      Assim como para ajuste linear, os parâmetros que abrangem a função nls envolvem:

args(nls)

## function (formula, data = parent.frame(), start, control = nls.control(), 
##     algorithm = c("default", "plinear", "port"), trace = FALSE, 
##     subset, weights, na.action, model = FALSE, lower = -Inf, 
##     upper = Inf, ...) 
## NULL

      Além do pacote incluido na distribuição básica do R e que permite ajustes não-lineares (stats), existem diversos outros que permitem ajustes com algoritmos, avaliações e plotagens variadas, tais como nlme (mixed-effects), nlrwr, nlstools, nls2, nls.multstart, minpack.lm (algoritmo de Levenberg-Marquadt), nlshelper, e nlsLM.

5.3.2 Algumas vantagens do modelo linear sobre o não-linear

  Ainda que a estimativa de parâmetros de modelos não lineares seja mais precisa utilizando-se ajustes também não lineares, o algoritmo linear oferece algumas vantagems, entre as quais:

1. É mais fácil, com algoritmo simplificado, e mesmo pelo uso de somatórias de algumas quantidades envolvendo x e y, sendo resolvido com calculadora científica simples, ou mesmo à mão;
2. é mais intuitivo visualmente, posto que o modelo final será sempre uma reta;
3. possui apenas dois parâmetros na equação, intercepto e inclinação;
4. requer poucas medidas, já que uma reta se constroi com apenas dois pontos;
5. não requer sementes para estimativas iniciais o que, a depender do modelo não-linear, pode ser bem abstrato, culminando em mínimos locais ou mesmo na falta de solução para o ajuste;
6. permite interpretação experimental quando há fuga da linearidade;
7. independe de um modelo físico específico;
8. não requer, por vezes, a necessidade de constrição de resultados (constraints), por exemplo instruindo o algoritmo a buscar uma estimativa obrigatoriamente de valor positivo para o parâmetro.
9. relações lineares e transformações são encontradas em inúmeros modelos físicos nas Ciências Naturais.

5.4 Enzimas alostéricas

      A alosteria constitui um dos principais recursos da metabolismo para a regulação dos níveis de compostos celulares. De etiologia grega (allos = outro, stereos = estrutura), uma enzima alostérica é aquela que altera seu perfil catalítico em função de transições conformacionais mediadas por moléculas que interagem fora de seu sítio ativo, sejam elas substrato, coenzimas, ou outros compostos (Traut 2007). O efeito resultante constitui em uma modulação da atividade enzimática, quer ativando-a ou inibindo-a. Enzimas alostérica comportam-se portanto como enzimas regulatórias em uma rota metabólica, e cuja atividade pode ser modulada em função de retroinibição ou inibição por feedback, bem como por ativação pelo precursor (Leone 2021).
      A equação que define uma enzima alostérica em função do teor de seu substrato dada abaixo:

\[\begin{equation} v=\frac{Vm*S^n}{(Km^n+S^n)} \tag{5.3} \end{equation}\]

Onde nH representa o coeficiente de cooperatividade ou constante de Hill para a ligação com moléculas de S (de maneira similar à ligação de \(O_{2}\) à hemoglobina. De modo geral, o valor de nH pode ser inferior à unidade (cooperatividade negativa) ou superior a essa (cooperatividade positiva). Para ilustrar o comportamento cinético de uma enzima alostérica, segue o trecho abaixo, que também introduz outro formato para representar curvas no R nomeando a variável independente (x).

v = function(S, Vm=10, Km=3, nH=2) {Vm*S^nH/(Km^nH+S^nH)}
curve(v,from=0,to=10,n=100, xlab="S", ylab="v",
      bty="L") # eixos em L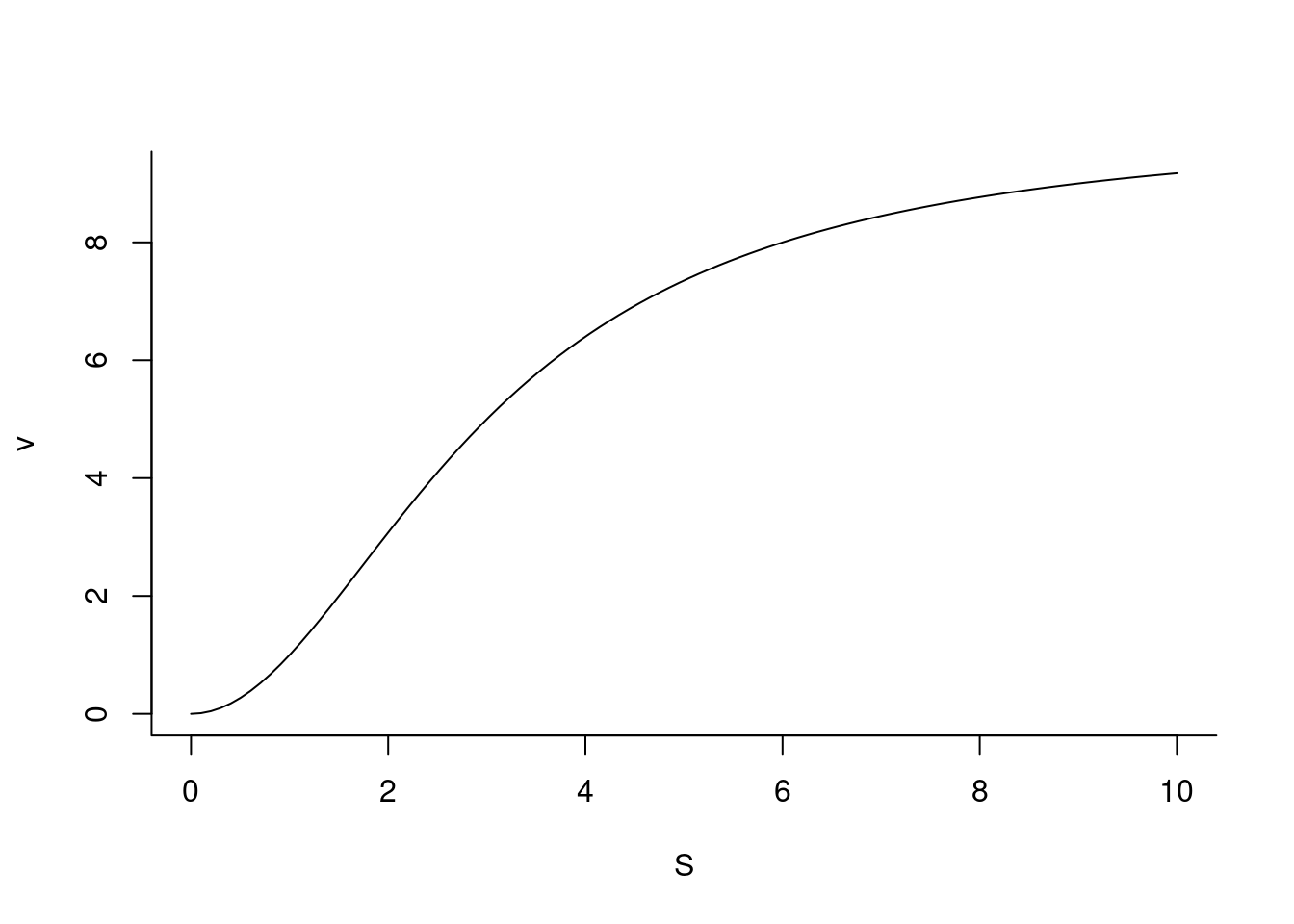

  Interessante também observar como o perfil enzimático alostérico se define frente à variação do coeficiente nH.

nH=seq(from=0.1,to=3,length.out=7) # sequência para 7 valores de nH
for(i in 1:length(nH)) { # loop para adicionar curva alostérica a cada valor de nH
  add<-if(i == 1) FALSE else TRUE # controle de fluxo
  v = function(S, Vm=10, Km=3, a=nH[i]) {Vm*S^a/(Km^a+S^a)}
  curve(v,from=0,to=4, n=500, col=i, xlab="S", ylab="v",
        bty="L", add=add)
}
arrows(0,5,3,2,length=0.1,angle=45, col="blue") # seta para nH
text(0.5,5.2,"nH",col="blue") # indexador para nH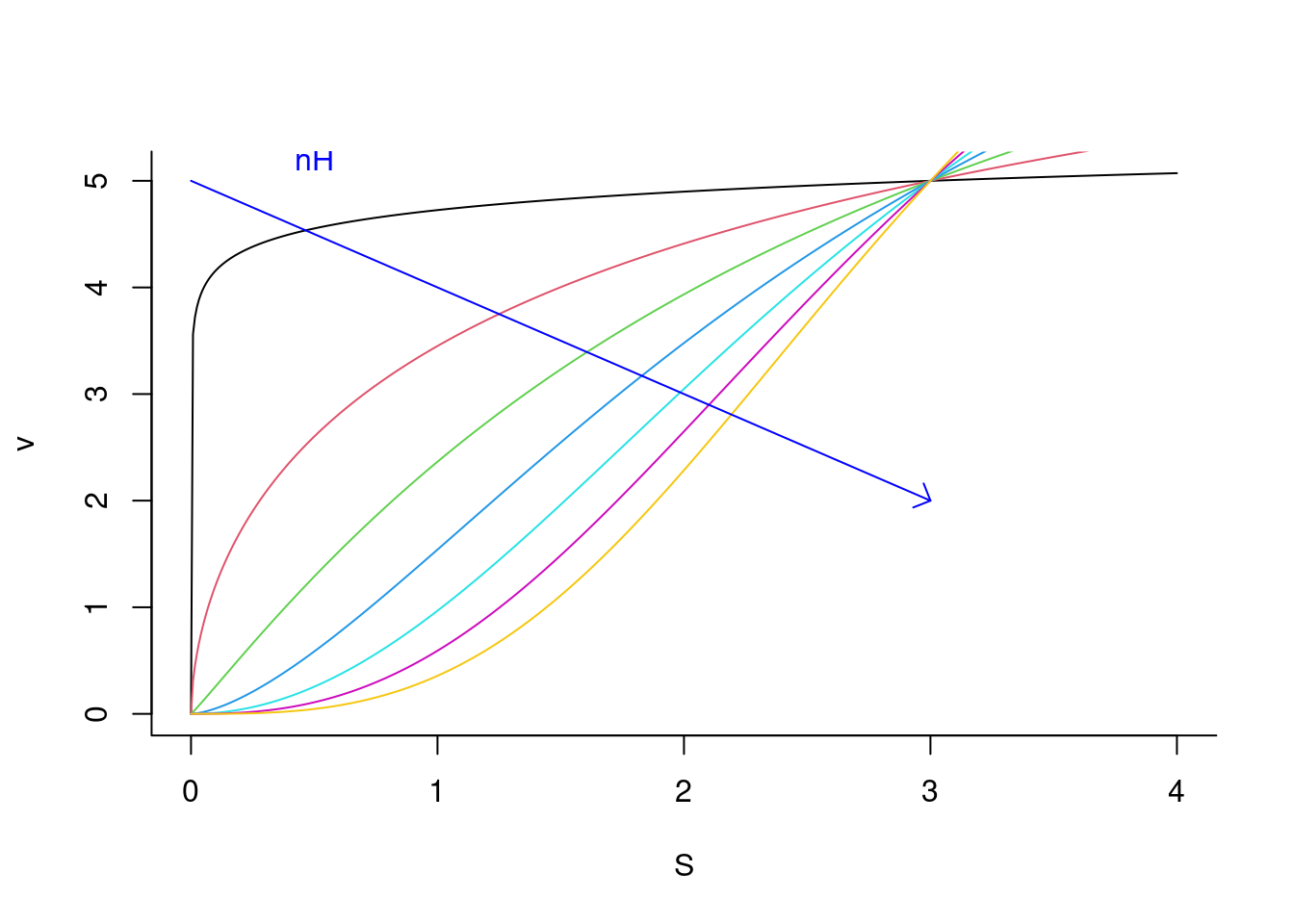

Figura 5.13: Perfil alostérico de uma enzima sob variação do coeficiente de cooperatividade nH.

5.5 Inibição Enzimática

      Capítulo vasto na enzimologia e com aplicação direta em Química, Farmacologia, Biotecnologia, Biomedicina e áreas afins, a inibição enzimática encontra-se no âmago dos fármacos, medicamentos e biosensores. Sob um ponto de vista simplificado, a atividade enzimática pode ser reduzida na presença de vários efetores, entre moléculas endógenas ou exógenas do metabolismo celular, incluindo o próprio substrato. Genericamente a inibição enzimática classifica-se como irreversível quando a ativide decai pela ligação covalente de um inibidor, ou reversível, quando há um equilíbrio de associação/dissociação com a macromolécula. A seguir serão ilustradas inibições reversíveis.

5.5.1 Inibição pelo substrato

      Uma inibição enzimática comum ao metabolismo é a protagonizada pelo próprio substrato em excesso no meio, sendo definida por:

\[\begin{equation} v=\frac{Vm*S}{S(1+\frac{S}{Ks})+Km} \tag{5.7} \end{equation}\]

      Dessa forma, o gráfico resultante de uma inibição por excesso de substrato pode ser reproduzido por:

S=seq(0,10,0.1)
v_alos <- function(S, Vm=10, Km=0.5, Ks=2) {Vm*S/(S*(1+S/Ks)+Km)}
curve(v_alos, xlim=c(0,10), xlab="S",ylab="v")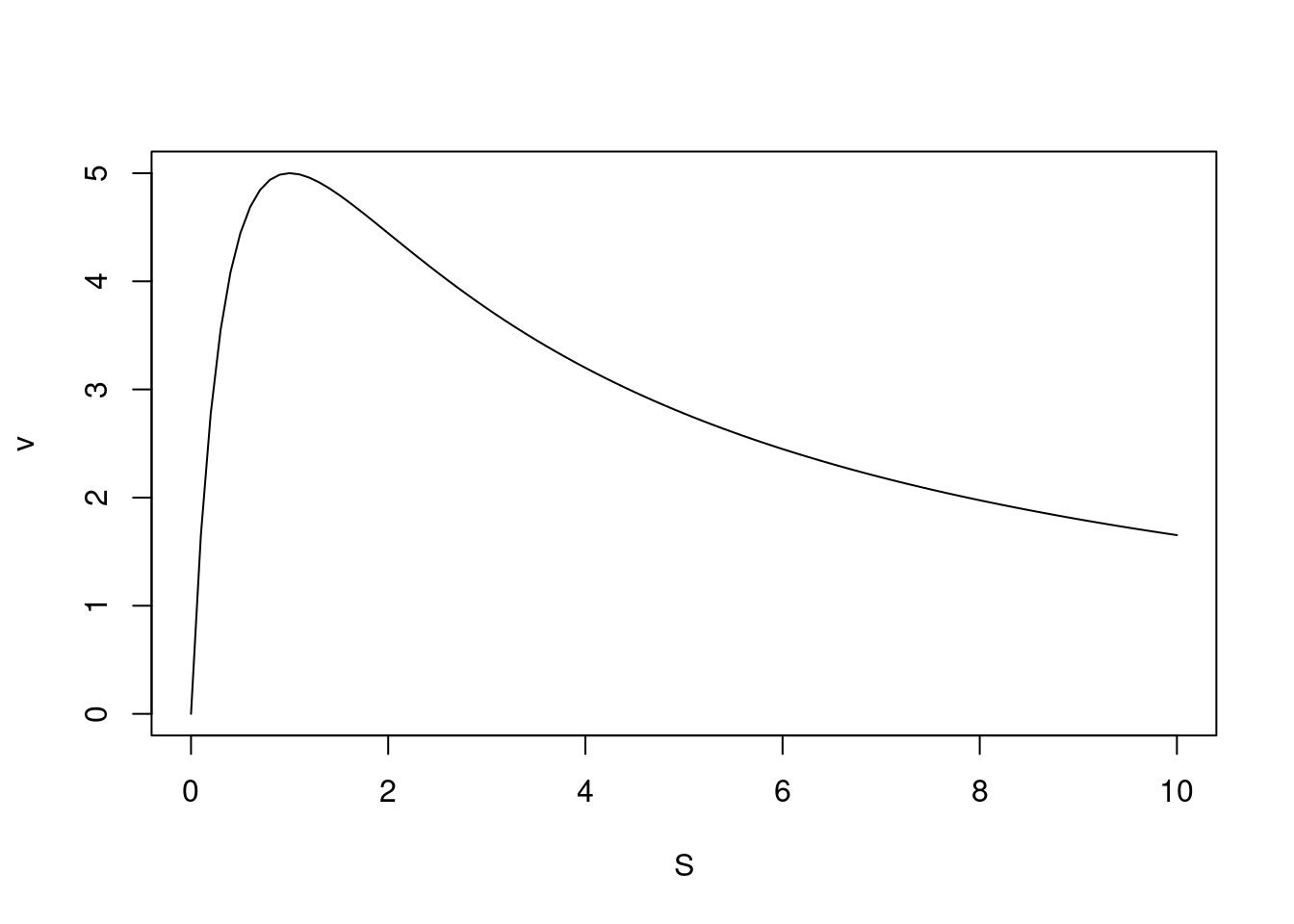

Figura 5.14: Comportamento cinético de uma enzima inibida por excesso de substrato.

      Percebe-se pela figura 5.14 que a atividade da enzima alcança um limite sendo reduzida com o aumento do teor de substrato.

5.5.2 Modelos de inibição enzimática

      A inibição de enzimas por moléculas que não o próprio substrato pode ser representada por um diagrama no qual o efetor altera um dos elementos representados na equação (5.1), tal como na figura abaixo.

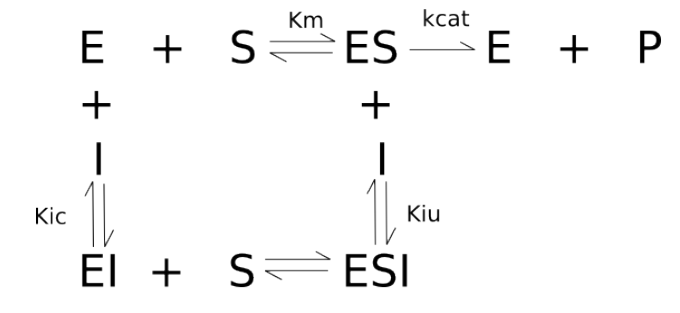
Figura 5.15: Diagrama representativo dos tipos de inibição enzimática. kcat: constante catalítica; Ki: constante de equilíbrio de dissociação do inibidor, com índices para inibição competitiva (Ki), incompetitiva (Kiu) e não competitiva (Kic e Kiu).

      Nesse caso, pode-se definir os três tipos principais de inibição enzimática reversível como inibição competitiva, incompetitiva e não competitiva (pura ou mista). Em síntese, a inibição competitiva dá-se quando o inibidor complexa-se ao sítio ativo da enzima; a inibição incompetitiva, quando o inibidor interage com o complexo enzima-substrato; e a inibição não competitiva, quando o inibidor liga-se em outro local que não o sítio ativo da enzima, podendo ainda ser pura (Kiu = Kic) ou mista (Kiu > ou < Kic).
      Um modelo matemático que abrange esses três tipos de inibição enzimática é descrito na equação abaixo:

\[\begin{equation} v=\frac{Vm*S}{Km(1+\frac{I}{Kic})+S(1+\frac{I}{Kiu})} \tag{5.8} \end{equation}\]

      Dessa forma, a equação (5.8) reduz-se em seus termos multiplicadores no denominador, em função do tipo de inibição enzimática presente, até o modelo primitivo de Michaelis-Mentem, quando na ausência do inibidor.

5.5.2.1 Curva de Michaelis-Mentem para modelos de inibição enzimática

      Podemos simular no R as cuvas michaelianas para modelos clássicos de inibição, considerando valores para as constantes de equilíbrio de dissociação dos inibidores como Kic = 0.2, e Kiu = 1, como no trecho de código abaixo.

par(mfrow=c(2,2)) # divide a área de plotagem
S=seq(0,10,0.1) # geração de teores de S
contr <- function(S,Vm=10,Km=0.5) {Vm*S/(Km+S)} # função de MM, sem inibição
curve(contr, xlim=c(0,10), xlab="S",ylab="v",main="Competitiva") # cuva controle; veja que o título tem que ser adicionado para a 1a. de par de curvas, controle e inibição

# Modelos de inibição:

# Competitiva
comp.i <- function(S, Vm=10, Km=0.5, I=2, Kic=0.2) {Vm*S/(Km*(1+I/Kic)+S)}
curve(comp.i, add = TRUE, col="red",lty=2) # competitiva

# Não competitiva pura
pura.i <- function(S, Vm=10, Km=0.5, I=2, Ki=1) {Vm*S/(Km*(1+I/Ki)+S*(1+I/Ki))}
curve(contr, xlim=c(0,10), xlab="S",ylab="v",main="Não Compet. Pura") 
curve(pura.i, add = TRUE, col="red",lty=2) # não competitiva pura (Kiu=Kic=Ki)

# Não competitiva mista
mista.i <- function(S, Vm=10, Km=0.5, I=2, Kic=0.2, Kiu=1) {Vm*S/(Km*(1+I/Kic)+S*(1+I/Kiu))}
curve(contr, xlim=c(0,10), xlab="S",ylab="v",main="Não Compet. Mista") 
curve(mista.i, add = TRUE, col="red",lty=2) # não competitiva mista

# Incompetitiva
incomp.i <- function(S, Vm=10, Km=0.5, I=2, Kiu=1) {Vm*S/(Km+S*(1+I/Kiu))}
curve(contr, xlim=c(0,10), xlab="S",ylab="v",main="Incompetitiva") 
curve(incomp.i, add = TRUE, col="red",lty=2) # incompetitiva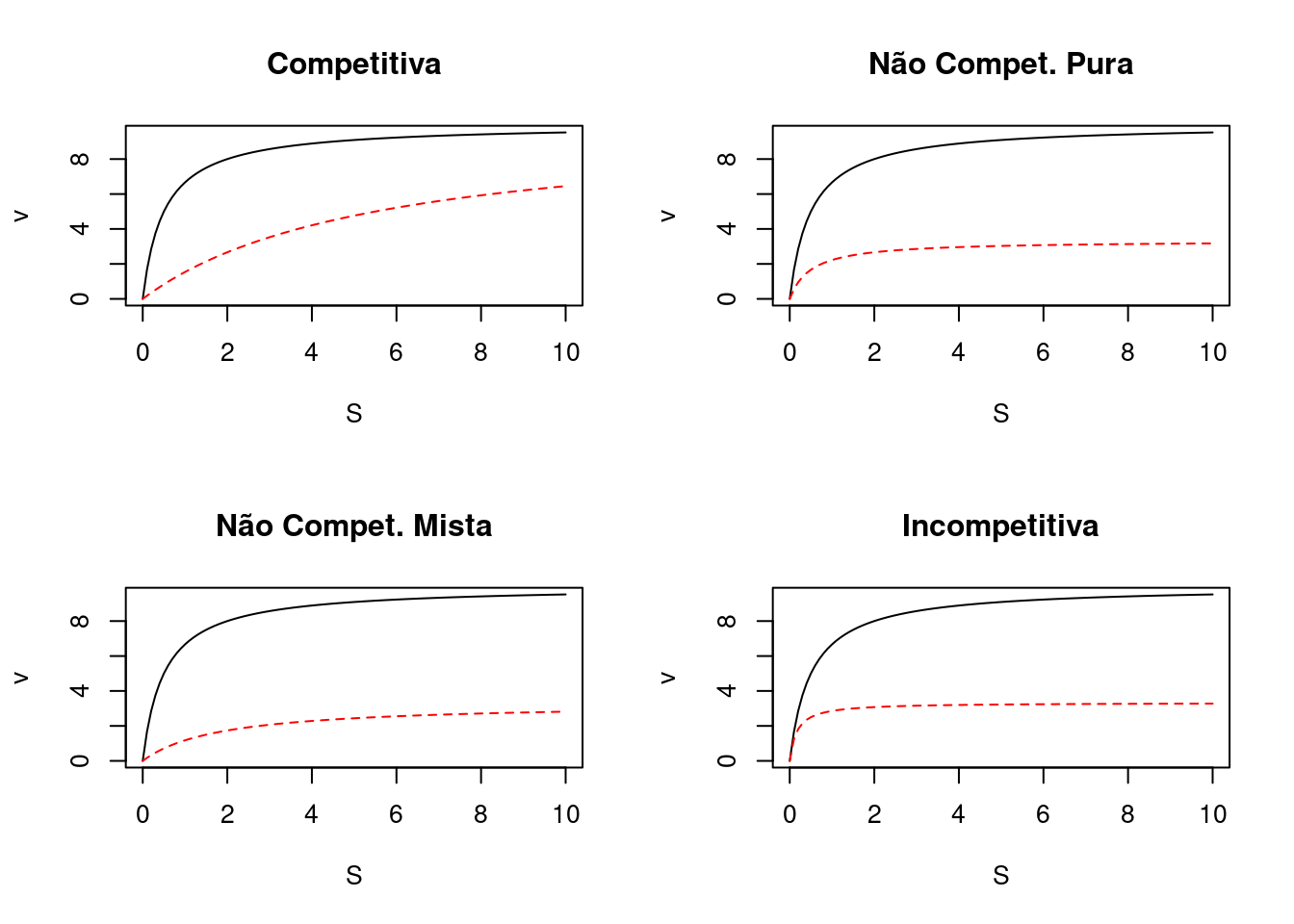

Figura 5.16: Curva de Michaelis-Mentem na presença de inibidores de comportamento clássico.

layout(1) # retorna à janela gráfica original

      Perceba que para o modelo competitivo a velocidade limite Vm da reação tende a ser alcançada, já que a ocupação do sítio ativo da enzima é mutualmente exclusiva entre substrato e inibidor, privilegiando o primeiro quando em alto teor. Por outro lado, o valor de Vm não é tangível para os demais modelos de inibição, já que o inibidor se liga em outro sítio na enzima (não competitivo) ou ao próprio substrato (incompetitivo). Para visualizar alterações nos gráficos, experimente modificar os parâmetros da simulação (Vm, Km, Ki, Kic, Kiu, I).
      Ainda que seja possível um discernimento do modelo competitivo dos demais, perceba também que isso só foi possível por uma simulação que empregou um teor S 20 vezes maior que o valor de Km da reação. Isso nem sempre é possível na prática, como elencado abaixo, já que o emprego de altos teores de S:

1. Agrega maior custo financeiro ao ensaio.
2. Pode resultar em inibição por excesso de substrato.
3. Pode elevar a viscosidade do meio, reduzindo a taxa catalítica.

      Percebe-se, da figura 5.16 e das observações acima, a dificuldade em classificar o tipo de inibição enzimática baseado na observação direta de uma curva de Michaelis-Mentem.

5.5.2.2 Diagnóstico de modelos de inibição enzimática por Lineweaver-Burk

      As transformações lineares da equação de Michaelis-Mentem são muito úteis no diagnóstico visual de modelos de inibição. Nesse sentido, o emprego da linearização por duplos-recíprocos para esses modelos resutará nas equações de inibição que seguem:

\[\begin{equation} \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S} \quad ;\, competitivo \tag{5.9} \end{equation}\] \[\begin{equation} \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Ki})}{Vm}*\frac{1}{S(1+\frac{I}{Ki})} \quad ;\, puro \tag{5.10} \end{equation}\] \[\begin{equation} \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, misto \tag{5.11} \end{equation}\] \[\begin{equation} \frac{1}{v}=\frac{1}{Vm}+\frac{Km}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, incompetitivo \tag{5.12} \end{equation}\]

      Observe que os termos multiplicadores inseridos em S e Km na equação de duplo-recíproco apenas alteram seu formalismo apresentado equação (5.3). Dessa forma, os modelos de inibição enzimática podem ser ilustrados pelo R junto à transformação de Lineweaver-Burk (ou qualquer outra), como abaixo.

# Substrato e Inibidor
S=seq(0.1,10,length=10) # cria um vetor para substrato
I = 2 # concentração de inibidor

# Parâmetros cinéticos:
Km=0.5
Vm=10
Kic=0.2
Ki=0.2
Kiu=1

# Equações
v=Vm*S/(Km+S) # equação de MM
v.comp=Vm*S/(Km*(1+I/Kic)+S) # competitivo
v.puro=Vm*S/(Km*(1+I/Ki)+S*(1+I/Ki)) # não competitivo puro
v.misto=Vm*S/(Km*(1+I/Kic)+S*(1+I/Kiu)) # não competitivo misto
v.incomp=Vm*S/(Km+S*(1+I/Kiu))

# Gráficos
par(mfrow=c(2,2)) # área de plot pra 4 gráficos

plot(1/S,1/v,type="l",main="Competitivo",ylim=c(0,2))
points(1/S,1/v.comp, type="l",col="red")
plot(1/S,1/v,type="l",main="Puro",ylim=c(0,5))
points(1/S,1/v.puro, type="l",col="red")
plot(1/S,1/v,type="l",main="Misto",ylim=c(0,2))
points(1/S,1/v.misto, type="l",col="red")
plot(1/S,1/v,type="l",main="Incompetitivo",ylim=c(0,1))
points(1/S,1/v.incomp, type="l",col="red")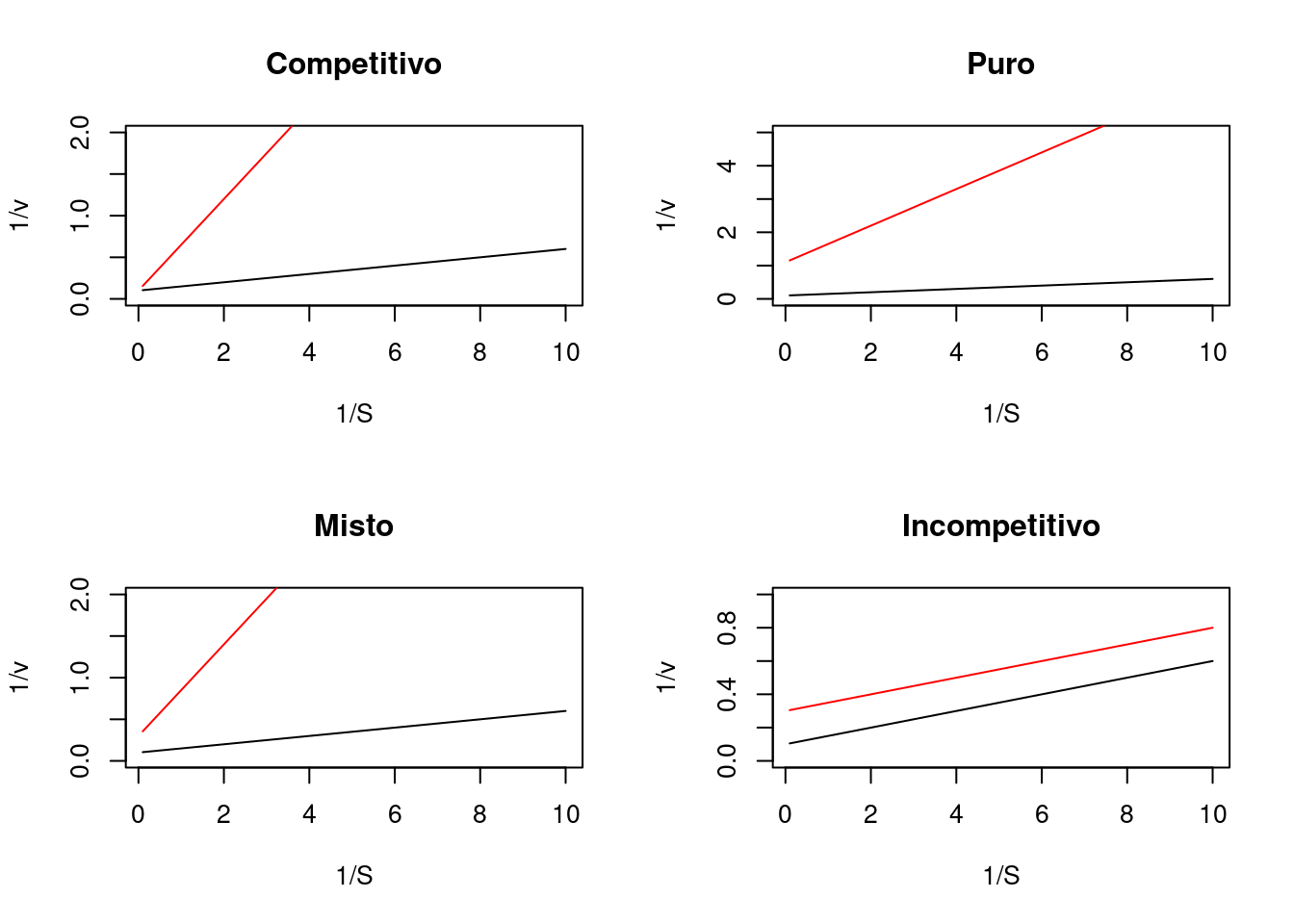

Figura 5.17: Diagnóstico de modelos de inibição enzimática por Lineweaver-Burk.

layout(1) # volta à janela gráfica normal

      Agora a distinção de modelos de inibição se torna mais evidente pela linearização. Assim como mencionado para os modelos representados na equação direta de Michaelis-Mentem, pode-se variar os parâmetros cinéticos e experimentar a visualização dos duplos-recíprocos.
      Novamente, ainda que a linearização permita um melhor diagnóstico do tipo de inibição presente, o ajuste não linear é mais adequado para a determinação das constantes de inibição (Ki’s), uma vez que não agrega os erros advindos das transformações lineares (embora a inserção de pesos estatísticos possa aliviar a imprecisão dos resultados).

5.5.2.3 Ki & IC\(_{50}\)

      A concentração inibitória a 50% do teor de inibidor, definida como IC\(_{50}\), pode ser determinada empiricamente sem o conhecimento dos parâmetros de catálise enzimática envolvidos. Para isso, basta se obter um valor de inibição relativa num ensaio a concentração fixa de S, variando-se o teor de inibidor. De fato, análogos ao IC\(_{50}\) existem em ampla gama nas Ciências Naturais, não envolvendo necessariamente qualquer informação cinética ou termodinâmica dos compostos envolvidos, mas tão somente a informação empírica do resultado. Exemplificando, os parâmetros DE\(_{50}\) (dose efetiva) ou DL\(_{50}\) (dose letal), e mesmo projeções de X\(_{50}\), tal como Tm (temperatura de desnaturação a 50%), e o valor de pKa em tampões (pH em que as espécies encontram-se 50% ionizadas/protonadas em solução).
  No entanto, existe uma relação útil entre a constante de equilíbrio de dissociação do inibidor Ki e o valor de IC\(_{50}\) que permite sua permuta, desde que conhecido o modelo de inibição (Yung-Chi and Prusoff 1973). Generalizando para os modelos de inibição, pode-se definir uma equação geral pra relação de Cheng-Prusoff como:

\[\begin{equation} IC_{50} = \frac{(1+\frac{S}{Km})}{(\frac{1}{Kic})+(\frac{1}{Km*Kiu})} \tag{5.13} \end{equation}\]

      Exemplificando, para um modelo competitivo de inibição, onde Kiu é nulo:

\[\begin{equation} IC_{50} = Kic(1+\frac{S}{Km}) \tag{5.14} \end{equation}\]

   Como acima mencionado, o valor de IC\(_{50}\) pode ser obtido a partir de dados experimentais de inibição relativa (v/Vm, por ex) em diferentes concentrações de inibidor fixando um valor de S. Nesse caso, podemos ilustrar no R a obtenção de IC\(_{50}\), utilizando-se um ajuste não linear para a equação de quatro parâmetros que segue (curva de Rodbard, DeLean, Munson, and Rodbard (1978)).

\[\begin{equation} ativ. residual \, \% =\frac{v}{Vm} = inf+\frac{sup-inf}{1+log(\frac{I}{IC_{50}})^{nH}}) \tag{5.15} \end{equation}\]

logI.nM <- c(5.5,5.2,4.9,4.6,4.3,3.7,3.3,3,2.8) # conc. de I, em unidade log10
ativ.res <- c(0.02,0.07,0.12,0.22,0.36,0.53,0.67,0.83,0.85) # ativ. residual, v/Vm
dados <- data.frame(logI.nM,ativ.res) # criação do dataframe
plot(ativ.res~logI.nM, dados) # plot dos dados
ic50.fit <- nls(formula(ativ.res ~ inf+(sup-inf)/(1+(logI.nM/logIC50)^nH)),algorithm="port", data=dados,start=list(inf=0, sup=0.80, logIC50=4,nH=10), lower=c(inf=-Inf, sup=-Inf, logIC50=0, nH=-Inf) ) # ajuste não linear
summary(ic50.fit) # sumário do ajuste

## 
## Formula: ativ.res ~ inf + (sup - inf)/(1 + (logI.nM/logIC50)^nH)
## 
## Parameters:
##         Estimate Std. Error t value Pr(>|t|)    
## inf       -0.321      0.293   -1.09   0.3235    
## sup        1.120      0.231    4.85   0.0047 ** 
## logIC50    4.081      0.231   17.67  1.1e-05 ***
## nH         4.054      1.746    2.32   0.0679 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03 on 5 degrees of freedom
## 
## Algorithm "port", convergence message: relative convergence (4)

lines(logI.nM,fitted(ic50.fit), col="blue") # linha ajustada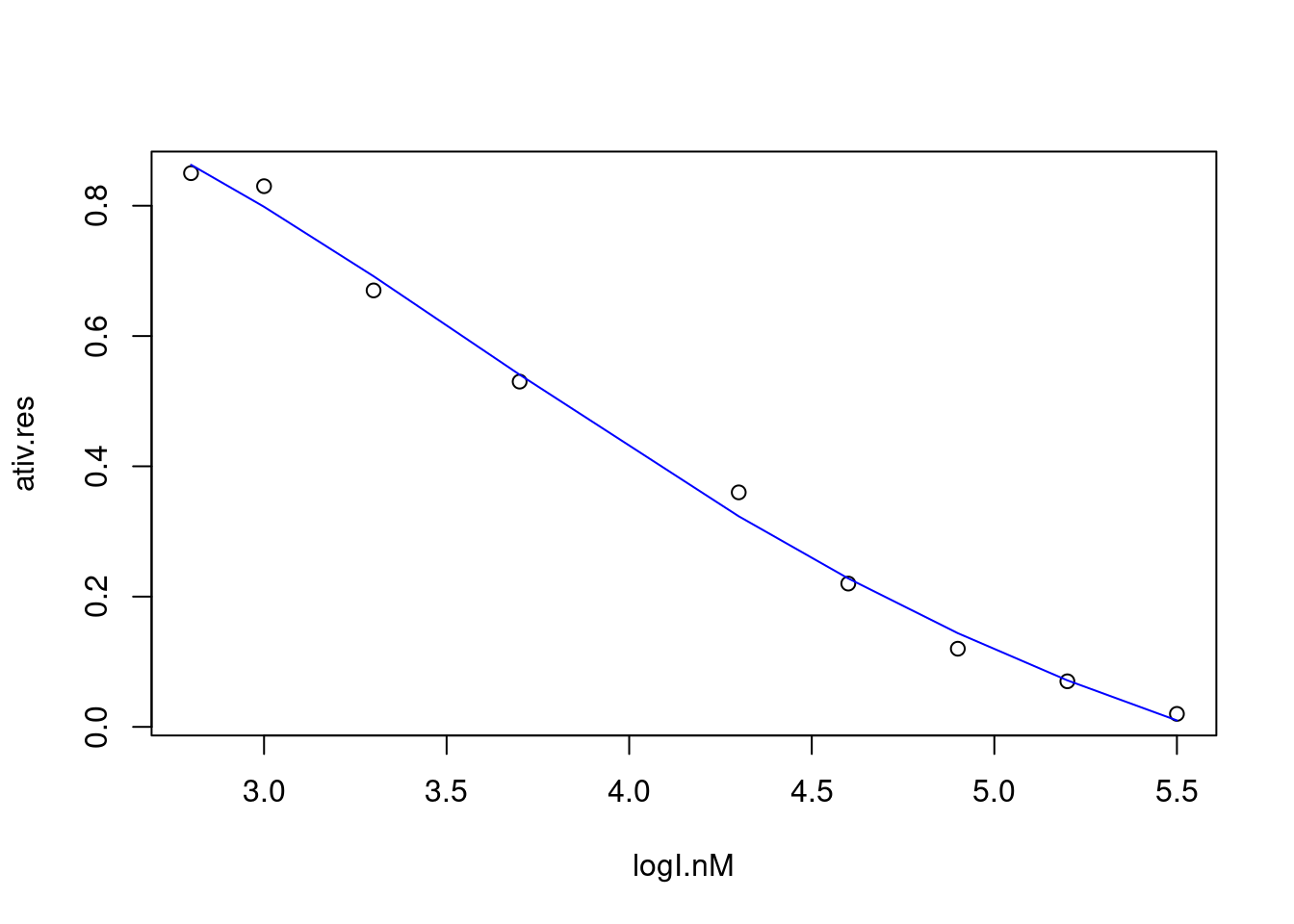

# E para extrair o valor de IC50...
IC50<-10^(coef(ic50.fit)[3]) # extração do 3o. parâmetro da tabela de ajuste, isto é: logIC50: 
IC50

## logIC50 
##   12042

      Perceba que o parâmetro de logIC50 foi extraído da tabela de ajuste não linear pelo comando coef. Isto é muito útil quando desejamos utilizar um coeficiente obtido em cálculos automáticos (programáveis), como veremos mais adiante. Por ora, faz-se interessante apresentar o parâmetro de IC50 obtido de forma mais elegante.
      Para isso, podemos utilizar duas funções do R para exprimir resultados quantitativos junto à caracteres (palavras, frases): print() e cat. O trecho de código abaixo ilustra esse output, e algumas diferenças.

cat("Valor de IC50 (nM):", IC50, "\n")

## Valor de IC50 (nM): 12042

print(paste("Valor de IC50 (nM):", IC50))

## [1] "Valor de IC50 (nM): 12042.0414863972"

      Basicamente, print exibe aspas e indexa o nome da coluna, enquanto cat os omite. Em adição, pode-se perceber outra variação no formato de impressão entre os dois comandos pelo exemplo abaixo:

print(paste("teores:",c(10,25,50)))

## [1] "teores: 10" "teores: 25" "teores: 50"

cat("teores:",c(10,25,50))

## teores: 10 25 50

      Outra possibilidade no R é a de se reduzir o número de casas decimais apresentados. Nesse caso, pode-se utilizar o comando round.

IC50<-10^(coef(ic50.fit)[3])
print(paste("Valor de IC50 (nM):", round(IC50,digits=2))) # arredondamento para duas casas decimais

## [1] "Valor de IC50 (nM): 12042.04"

      Mais uma vez, salienta-se a existência de alguns pacotes úteis do R para o cálculo de IC50, entre esse o pacote drc (dose-response curve).

5.6 Diagnóstico estatístico de inibição enzimática

      Em paralelo à inspeção visual dos gráficos de linearização para inibição enzimática, é possível validar-se um modelo sobre outro por uma análise de dispersão de erros dos modelos. Mas também é possível o emprego da função BIC ou da função AIC do R, e que respectivamente calculam valores para o Critério de Informação Bayseiano (Spiess and Neumeyer 2010) ou do Critério de Informação de Akaike (Akaike 1974). Em comum esse parâmetros calculam um valor relativo de informação não computada por um modelo avaliado. O menor valor encontrado para ambos espelha a solução do melhor modelo de ajuste.
      Matematicamente, BIC e AIC podem ser expressos como:

\[\begin{equation} BIC = p*ln(n)-2*ln(RSE)\\ \\ AIC = n*ln(\frac{RSE}{n})+2k+[\frac{2k(k+1)}{n-k-1}])\\ \tag{5.16} \end{equation}\]

|Onde p representa o no. de parâmetros do modelo, n o número total de pontos experimentais, k o fator p+1, e RSE o valor da soma dos quadrados dos resíduos (residual sum squares).

      Para exemplificar o uso desses parâmetros de qualidade do modelo estatístico, pode-se empregar um conjunto de dados contido no pacote nlstools, provendo o ajuste, plotagem, inspeção de resíduos, e aplicação de BIC e AIC:

library(nlstools)

## 
## 'nlstools' has been loaded.

## IMPORTANT NOTICE: Most nonlinear regression models and data set examples

## related to predictive microbiolgy have been moved to the package 'nlsMicrobio'

comp <- nls(compet_mich, vmkmki, list(Km=1,Vmax=20,Ki=0.5)) # ajuste competitivo, com dados, equação e sementes fornecidas pelo pacote nlstools
plotfit(comp, variable=1) # comando de plotagem do pacote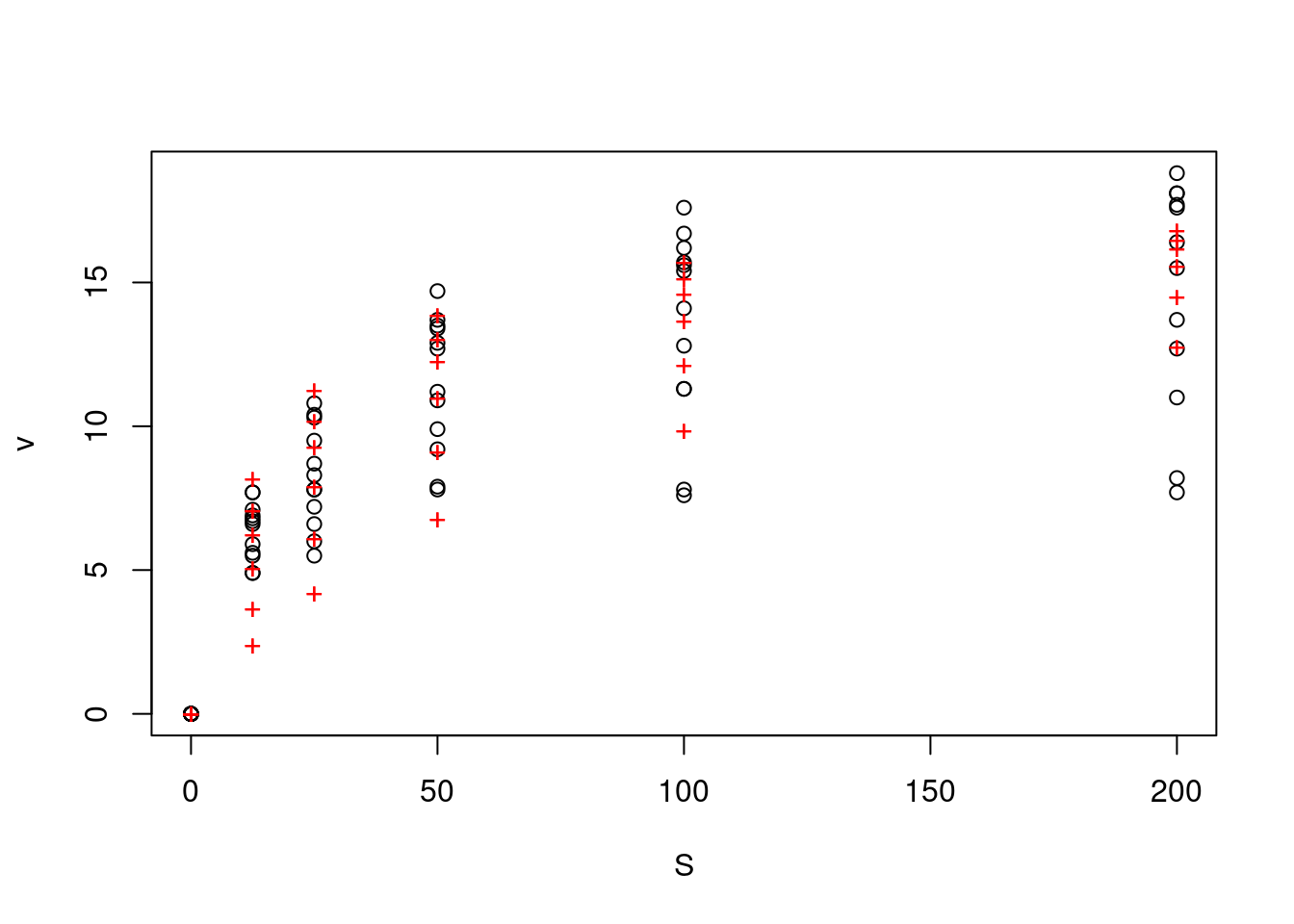

summary(comp)

## 
## Formula: v ~ S/(S + Km * (1 + I/Ki)) * Vmax
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## Km     15.214      2.501    6.08  5.8e-08 ***
## Vmax   18.056      0.629   28.71  < 2e-16 ***
## Ki     22.282      4.906    4.54  2.3e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2 on 69 degrees of freedom
## 
## Number of iterations to convergence: 11 
## Achieved convergence tolerance: 5.11e-06

res_comp <- nlsResiduals(comp) # resíduos do ajuste
plot(res_comp, which=1) # plotagem de resíduos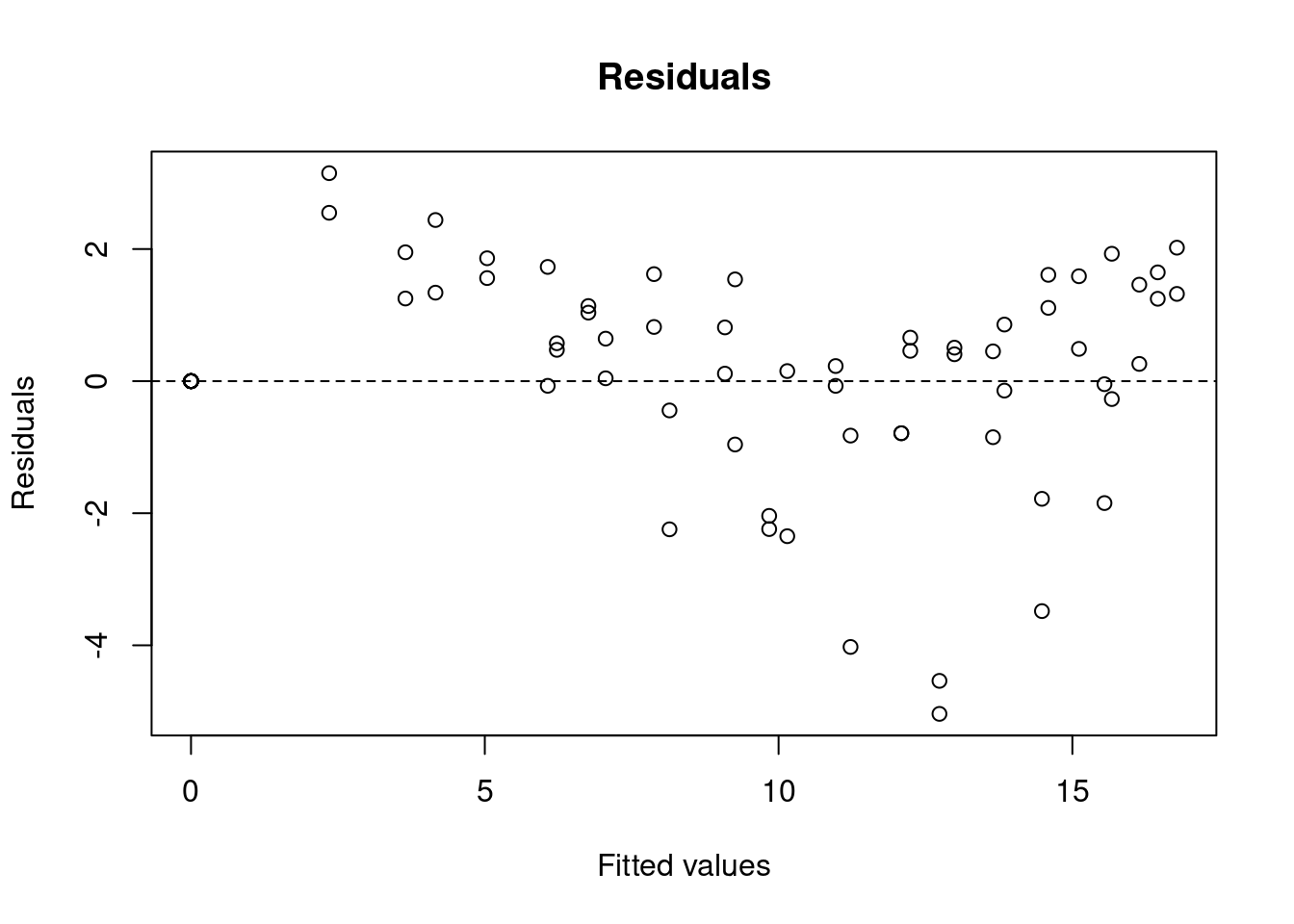

noncomp <- nls(non_compet_mich, vmkmki, list(Km=1, Vmax=20, Ki=0.5)) # o mesmo que acima, mas para o modelo não competitivo
plotfit(noncomp, variable=1)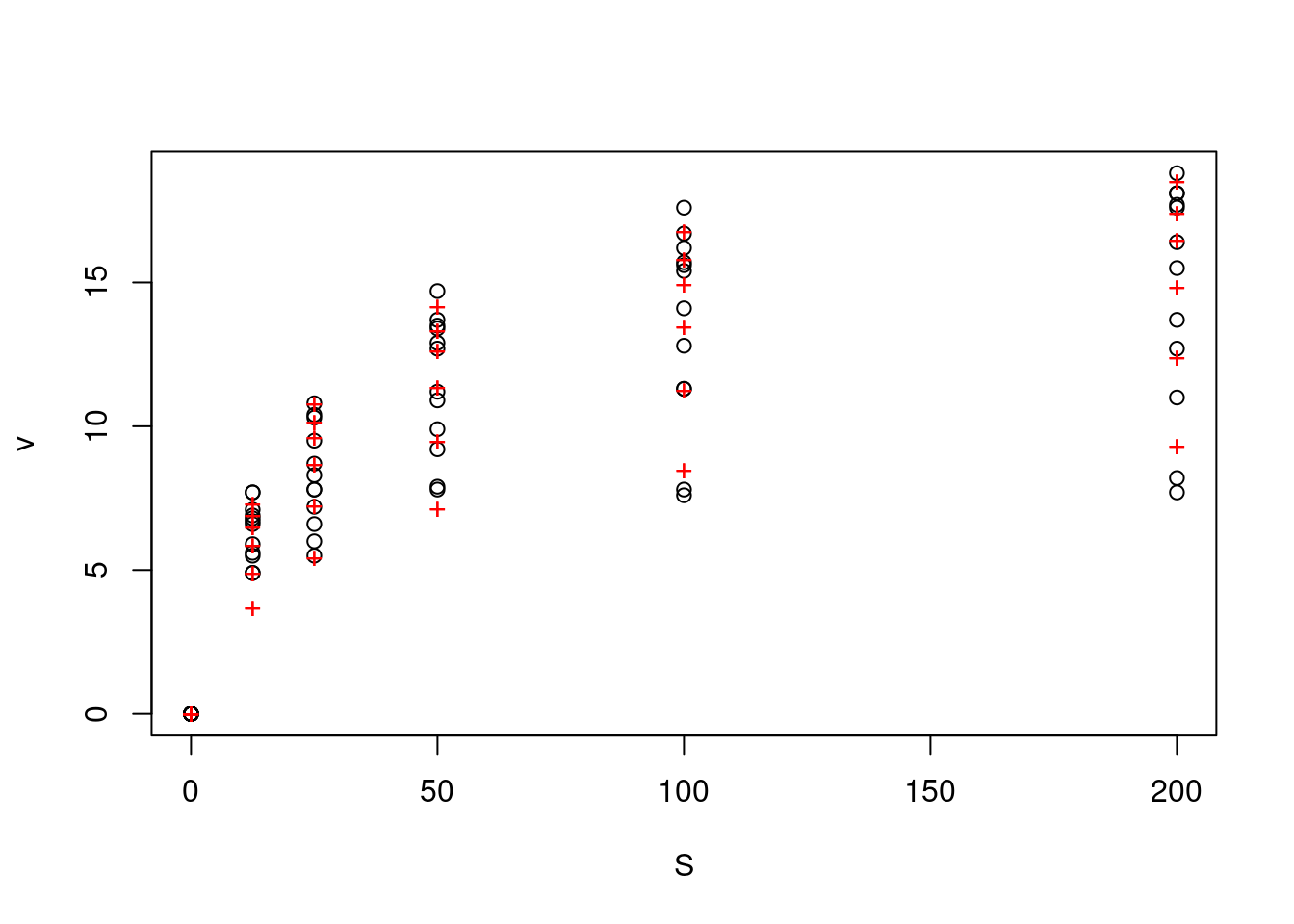

summary(noncomp)

## 
## Formula: v ~ S/((S + Km) * (1 + I/Ki)) * Vmax
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## Km     22.779      1.474    15.5   <2e-16 ***
## Vmax   20.587      0.431    47.8   <2e-16 ***
## Ki    101.356      7.330    13.8   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9 on 69 degrees of freedom
## 
## Number of iterations to convergence: 7 
## Achieved convergence tolerance: 8.25e-06

res_noncomp <- nlsResiduals(noncomp)
plot(res_noncomp, which=1)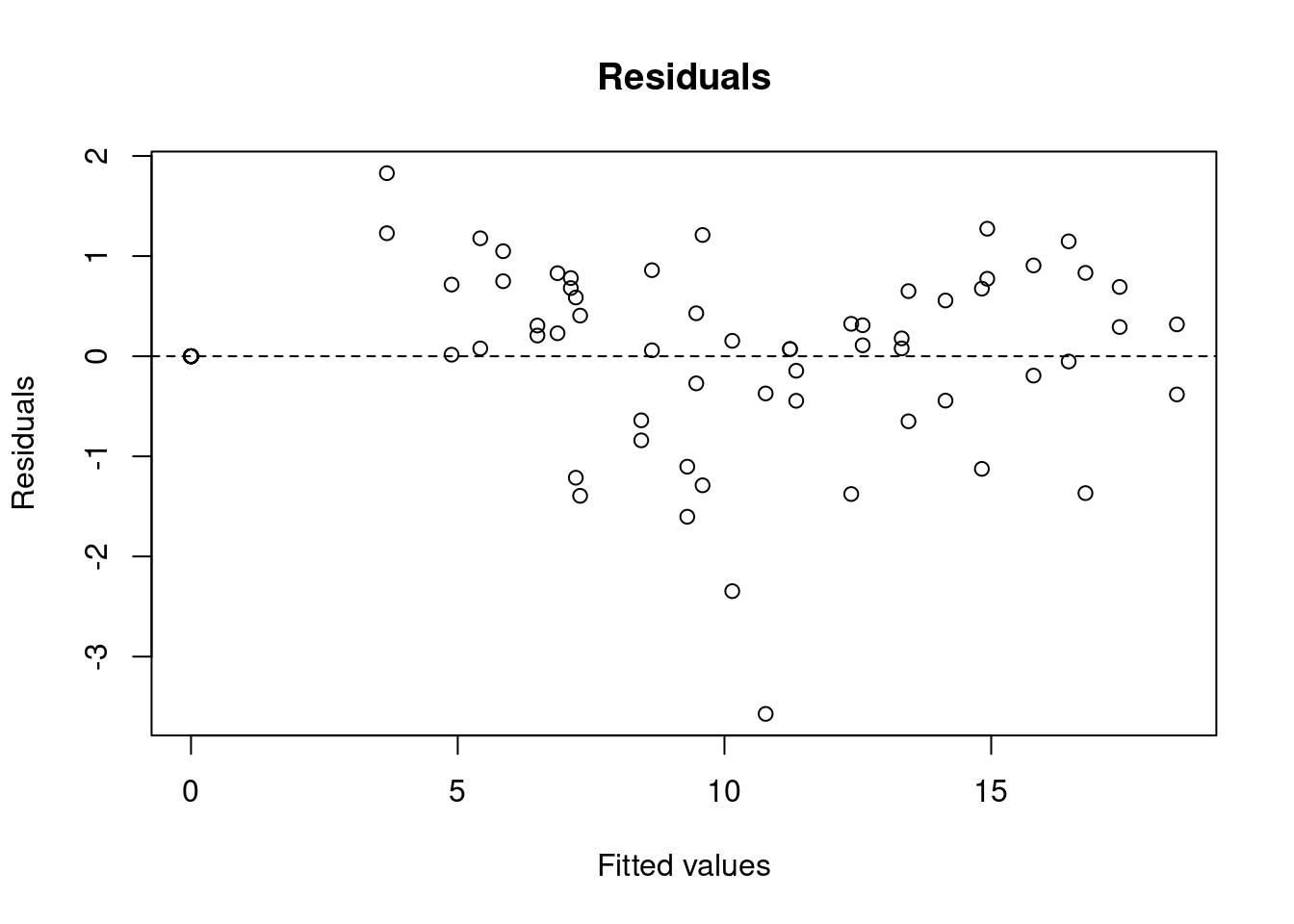

BIC(comp,noncomp) # Critério de informação de Baysean

##         df BIC
## comp     4 286
## noncomp  4 202

AIC(comp,noncomp) # Critério de informação de Akaike

##         df AIC
## comp     4 277
## noncomp  4 193

      Pode-se observar na comparação dos ajustes não lineares que o modelo não competitivo ajustou-se melhor que o modelo competitivo (valores menores para BIC e AIC)

5.7 Cinética de estado pré-estacionário

      Existem basicamente três tipos de comportamentos cinéticos para as enzimas: comportamento de Henry-Michaelis-Mentem-Briggs-Haldane, sucintamente denominado por michaeliano ou de estado estacionário (steady-state), comportamento de fase lag (quando o substrato leva algum tempo para ser convertido em produto), e comportamento de burst, transiente, ou de estado pré-estacionário (quando uma fase com rápida liberação de produto precede o estado estacionário). Algumas enzimas trabalham seguindo a cinética de burst, entre as quais algumas nucleosidades e glicosidases, e dehalogenases Tang et al. (2003).
      A cinética de estado pré-estacionário segue um formalismo um pouco distinto, e que depende do quantitativo de etapas reacionais. Exemplificando abaixo para uma reação de 3 etapas (Johnson 1992):

\[\begin{equation} E+S \begin{array}{c} _{k1}\\ \rightleftharpoons\\ ^{km1} \end{array} E*S \begin{array}{c} _{k2}\\ \rightleftharpoons\\ ^{km2} \end{array} E*P \begin{array}{c} _{k3}\\ \rightarrow \\ ^{}\end{array} E+P \tag{5.17} \end{equation}\]

      Nesse caso, as equações derivadas das observações experimentais, e que conduzem à determinação das constantes de velocidade são:

\[\begin{equation} kobs=k2+km2+k3 \tag{5.18} \end{equation}\] \[\begin{equation} Ao=\frac{k2*(k2+km2)}{kobs^2} \tag{5.19} \end{equation}\] \[\begin{equation} kcat=\frac{k2*k3}{kobs} \tag{5.20} \end{equation}\]

Onde kobs e Ao representam parâmetros experimentais de constante de velocidade observada e amplitude, respectivamente. Esses parâmetros podem ser obtidos a partir do ajuste não linear da equação abaixo aos dados experimentais:

\[\begin{equation} P=Ao(1-e^ {-kobs} + kcat * t) \tag{5.21} \end{equation}\]

      O trecho de código que segue simula uma curva de comportamento pré-estacionário, quando conhecidas as constantes de velocidade que determinam os parâmetros experimentais.

# Parâmetros
k2=387
km2=3
k3=22
xmin=0
xmax=0.075 # definição de limites para função

# Variáveis da equação de simulação (função dos parâmetros)
kobs=k2+km2+k3
Ao=k2*(k2+km2)/kobs^2
kcat=k2*k3/kobs

# Definição da função de simulação
sim=function(x,kobs,Ao,kcat){Ao*(1-exp(-kobs*x))+kcat*x}

# Curval de simulação
curve(sim(x,kobs=kobs,Ao=Ao,kcat=kcat),col="blue",
      type="o",xlim=c(xmin,xmax),cex=0.5,
      xlab="tempo", ylab="[P]")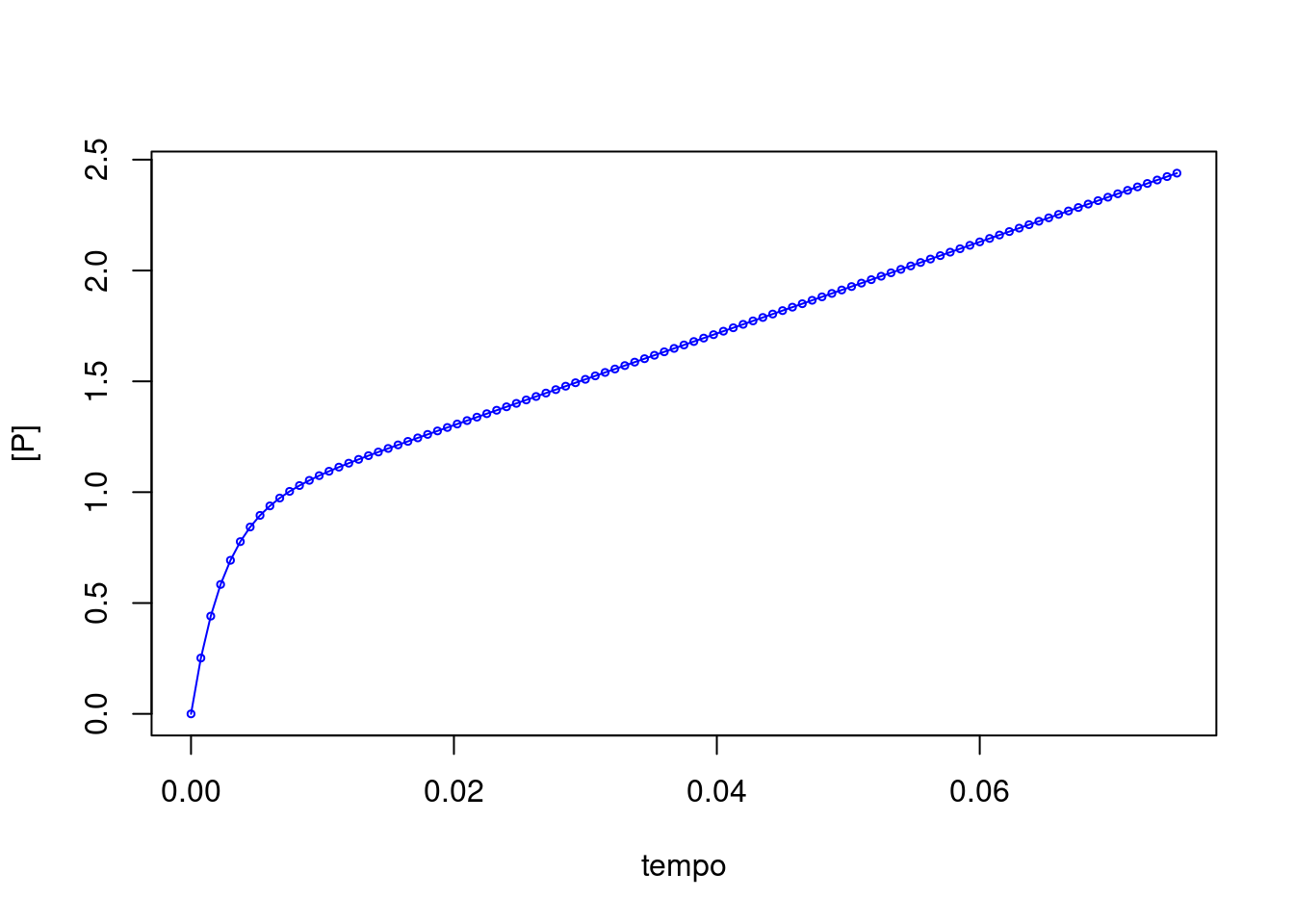

Figura 5.18: Formação de produto num modelo cinético de estado pré-estacionário.

      Note pela figura 5.18 que na cinética de estado transiente, existe uma fase pré-estacionária inicial eleva o teor de produto P rapidamente, e que antecede a fase estacionária de liberação constante de P.

      Por outro lado, por vezes é necessário o oposto, ou seja, determinar as constantes de velocidade a partir do conhecimento dos parâmetros experimentais kobs e Ao. Nesse caso (e em tantos outros transdisciplinares) o R possui funções de minimização que permitem encontrar a raíz de equações lineares ou não lineares.
      O procedimento envolve minimizar iterativamente um vetor de equações dadas as sementes para cada parâmetro. Para tal busca-se obter f(x) = 0 pela diferença entre um valor de referência; ou seja, quando a solução encontrar x quando f(x)-y = 0. Exemplificando, supondo que f(x) seja a+b/x, e que y seja 3. Então a busca se dá no sentido de encontrar a e b em a+b/x-3.
      Para a determinação das constantes de velocidade representadas na cinética transiente, vale mencionar a função optim em stats ou o pacote rootSolve, que buscam minimizar equações lineares e não lineares para encontrar os valores de seus parâmetros.
      Na solução dos parâmetros para estado pré-estacionário, ilustra-se abaixo o emprego do R com rootSolve, adicionando ainda a busca para Km como segue.

\[\begin{equation} Km = \frac{k3}{k2+k3} \tag{5.22} \end{equation}\]

# Cálculo de constantes cinéticas por solução de sistema de equações não lineares aplicadas à cinética de burst.

library(rootSolve) 
kobs =  0.06; Ao = 50; kcat = 300; Ks = 15
# define os parâmetros de ajuste não linear obtidos por curva progressiva experimental, t x P; 
# Obs: Ks obtido experimentalmente de curva de S x kobs

# Parâmetros
# x[1]=k2
# x[2]= k3
# x[3] = Km

# Modelo
model = function(x) c(x[1]/kobs^2-Ao,(x[1]*x[2])/kobs-kcat,Ks*x[2]/(x[1]+x[2])-x[3])
# o modelo acima deve conter uma lista de equações cuja igualdade é zero, ou seja, f(x)=0
(ss=multiroot(model,c(1,1,1))) # comando de execução do rootSolve (sementes pro algoritmo)

## $root
## [1]   0.2 100.0  15.0
## 
## $f.root
## [1]  0e+00  1e-13 -1e-09
## 
## $iter
## [1] 4
## 
## $estim.precis
## [1] 4e-10

      Os resultados da minimização podem ser interpretados como:

1. root = valores de xi pra f(xi)=0 ; ou seja, k2, k3, e Km;
2. f.root = valor de cada função pra cada xi (deve ser próximo de zero para cada);
3. iter = no. iterações ;
4. esti.precis = estimativa da precisão.

      A contemplar um capítulo ainda que extenso sobre cinética enzimática, existem inúmeros tópicos deixados de lado, dado o foco principal do emprego do R na solução de problemas quantitativos em biofísico-química. Dessa forma, omitimos diversos conceitos, tais como cinética lenta de interação de substrato (slow binding), cinética de múltiplos substratos (reação sequencial e ping-pong), equação integrada de Michaelis-Menten e curvas progressivas, ativação de moduladores, influência de pH e temperatura na catálise, e enzimas multisítios, entre vários.

References

Akaike, Hirotugu. 1974. “A New Look at the Statistical Model Identification.” IEEE Transactions on Automatic Control 19 (6): 716–23.

DeLean, A, PJ Munson, and Dl Rodbard. 1978. “Simultaneous Analysis of Families of Sigmoidal Curves: Application to Bioassay, Radioligand Assay, and Physiological Dose-Response Curves.” American Journal of Physiology-Endocrinology And Metabolism 235 (2): E97.

Johnson, Kenneth A. 1992. “1 Transient-State Kinetic Analysis of Enzyme Reaction Pathways.” In The Enzymes, 20:1–61. Elsevier.

Leone, Francisco de Assis. 2021. Fundamentos de Cinética Enzimática. Appris Ed.

Michaelis, L., and ML Menten. 1913. “Die Kinetik Der Invertinwirkung.” Biochem Z 49 (4): 333–69.

Scatchard, George. 1949. “The Attractions of Proteins for Small Molecules and Ions.” Annals of the New York Academy of Sciences 51 (4): 660–72.

Spiess, Andrej-Nikolai, and Natalie Neumeyer. 2010. “An Evaluation of R2 as an Inadequate Measure for Nonlinear Models in Pharmacological and Biochemical Research: A Monte Carlo Approach.” BMC Pharmacology 10 (1): 1–11.

Tang, Lixia, Jeffrey H Lutje Spelberg, Marco W Fraaije, and Dick B Janssen. 2003. “Kinetic Mechanism and Enantioselectivity of Halohydrin Dehalogenase from Agrobacterium Radiobacter.” Biochemistry 42 (18): 5378–86.

Traut, Thomas W. 2007. Allosteric Regulatory Enzymes. Springer Science & Business Media.

Wilkinson, GN. 1961. “Statistical Estimations in Enzyme Kinetics.” Biochemical Journal 80 (2): 324–32.

Yung-Chi, Cheng, and William H Prusoff. 1973. “Relationship Between the Inhibition Constant (KI) and the Concentration of Inhibitor Which Causes 50 Per Cent Inhibition (I50) of an Enzymatic Reaction.” Biochemical Pharmacology 22 (23): 3099–3108.